题目内容
在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE与BD的位置关系是 .
垂直
建立空间直角坐标系,利用坐标法解决.
以A为原点,AB,AD,AA1所在直线分别为x,y,z轴建立空间直角坐标系,如图,
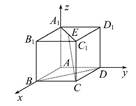
设正方体棱长为1,
则C(1,1,0),B(1,0,0),D(0,1,0),E( ,
, ,1),
,1),
∴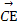 =(-
=(- ,-
,- ,1),
,1),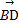 =(-1,1,0),
=(-1,1,0),
显然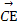 ·
·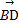 =
= -
- +0=0,
+0=0,
∴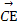 ⊥
⊥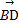 ,即CE⊥BD.
,即CE⊥BD.
以A为原点,AB,AD,AA1所在直线分别为x,y,z轴建立空间直角坐标系,如图,

设正方体棱长为1,
则C(1,1,0),B(1,0,0),D(0,1,0),E(
 ,
, ,1),
,1),∴
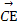 =(-
=(- ,-
,- ,1),
,1),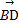 =(-1,1,0),
=(-1,1,0),显然
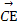 ·
·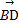 =
= -
- +0=0,
+0=0,∴
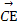 ⊥
⊥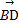 ,即CE⊥BD.
,即CE⊥BD.
练习册系列答案
相关题目
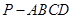 的底面为正方形,侧面
的底面为正方形,侧面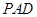
 底面
底面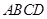 .
.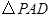 为等腰直角三角形,且
为等腰直角三角形,且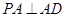 .
. ,
,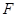 分别为底边
分别为底边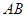 和侧棱
和侧棱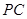 的中点.
的中点.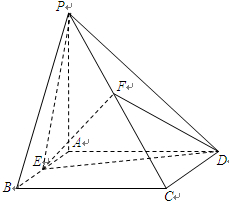
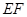 ∥平面
∥平面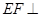 平面
平面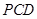 ;
; 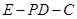 的余弦值.
的余弦值.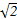 AB,E是SA的中点.
AB,E是SA的中点.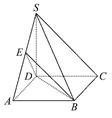
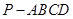 中,
中,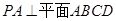 ,底面
,底面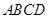 为梯形,
为梯形,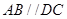 ,
,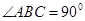 ,且
,且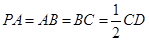 ,
,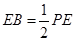 .
.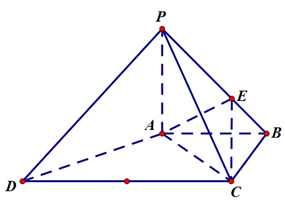
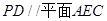 ;
;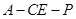 的余弦值.
的余弦值.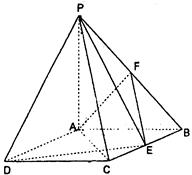
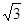 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.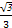 ,
,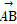 与
与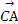 的夹角θ的大小是( )
的夹角θ的大小是( )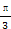
 π
π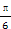
 π
π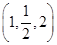 ,则m=________.
,则m=________.