题目内容
已知l∥α,且l的方向向量为(2,m,1),平面α的法向量为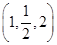 ,则m=________.
,则m=________.
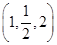 ,则m=________.
,则m=________.-8
(2,m,1)·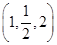 =0,得m=-8.
=0,得m=-8.
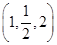 =0,得m=-8.
=0,得m=-8.
练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
题目内容
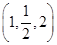 ,则m=________.
,则m=________.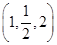 =0,得m=-8.
=0,得m=-8.
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案