题目内容
(本小题12分)如图:四棱锥P—ABCD中,底面ABCD
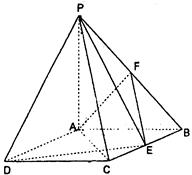
是矩形,PA⊥底面ABCD,PA=AB=1,AD=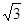 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.

是矩形,PA⊥底面ABCD,PA=AB=1,AD=
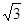 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.
(1)证明详见解析;(2) .
.
试题分析:(1)以A为原点,AD,AB,AP分别为x轴,y轴,z轴建立空间直角坐标系,求证 =0即可;(2)求出表示平面PDE的一个法向量
=0即可;(2)求出表示平面PDE的一个法向量 的坐标,由向量的夹角公式和已知条件可得到一个方程,解之即可.
的坐标,由向量的夹角公式和已知条件可得到一个方程,解之即可.
试题解析:解:(1) 建立如图所示空间直角坐标系,

则P(0,0,1),B(0,1,0),
 设
设
 ∴AF⊥PE
∴AF⊥PE
(2)设平面PDE的法向量为 ,由
,由 得
得 ,而
,而 ,
,
因为PA与平面PDE所成角的大小为45°,
所以sin45°= ,即
,即 ,得BE=x=
,得BE=x= ,
,
或BE=x= (舍去).
(舍去).
 .
.试题分析:(1)以A为原点,AD,AB,AP分别为x轴,y轴,z轴建立空间直角坐标系,求证
 =0即可;(2)求出表示平面PDE的一个法向量
=0即可;(2)求出表示平面PDE的一个法向量 的坐标,由向量的夹角公式和已知条件可得到一个方程,解之即可.
的坐标,由向量的夹角公式和已知条件可得到一个方程,解之即可.试题解析:解:(1) 建立如图所示空间直角坐标系,

则P(0,0,1),B(0,1,0),
 设
设
 ∴AF⊥PE
∴AF⊥PE (2)设平面PDE的法向量为
 ,由
,由 得
得 ,而
,而 ,
,因为PA与平面PDE所成角的大小为45°,
所以sin45°=
 ,即
,即 ,得BE=x=
,得BE=x= ,
,或BE=x=
 (舍去).
(舍去).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
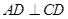 ,
,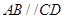 ,
,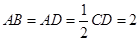 ,点M在线段EC上(除端点外)
,点M在线段EC上(除端点外)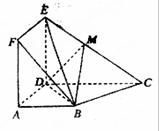
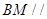 平面
平面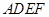 ;
;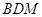 与平面ABF所成二面角为锐角,且该二面角的余弦值为
与平面ABF所成二面角为锐角,且该二面角的余弦值为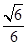 时,求三棱锥
时,求三棱锥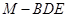 的体积
的体积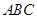 的底边
的底边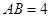 ,点
,点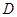 在线段
在线段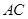 上,
上,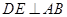 于
于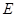 ,现将
,现将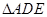 沿
沿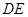 折起到
折起到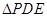 的位置(如图(2)).
的位置(如图(2)).
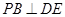 ;
;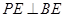 ,直线
,直线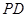 与平面
与平面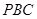 所成的角为
所成的角为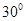 ,求
,求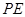 长.
长.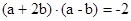 ,则a 与b的夹角为______
,则a 与b的夹角为______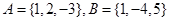 ,则
,则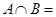 .
.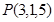 关于
关于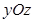 平面对称的点的坐标为( )
平面对称的点的坐标为( )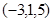
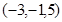
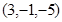
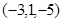
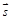 =(-1,1,1),平面π的法向量为
=(-1,1,1),平面π的法向量为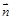 =(2,x2+x,-x),若直线l∥平面π,则x的值为___________.
=(2,x2+x,-x),若直线l∥平面π,则x的值为___________.