题目内容
(本小题满分12分)已知椭圆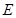 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在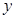 轴上,离心率
轴上,离心率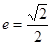 ,
,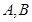 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且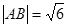 .
.
(Ⅰ)求椭圆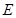 的方程;
的方程;
(Ⅱ)已知直线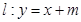 与椭圆
与椭圆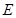 相交于
相交于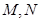 两点,且
两点,且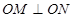 (其中
(其中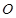 为坐标原点),求
为坐标原点),求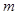 的值.
的值.
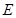 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在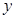 轴上,离心率
轴上,离心率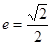 ,
,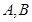 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且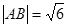 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)已知直线
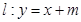 与椭圆
与椭圆 相交于
相交于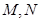 两点,且
两点,且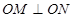 (其中
(其中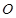 为坐标原点),求
为坐标原点),求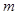 的值.
的值.(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
试题分析:(1)设椭圆的方程为
 (
(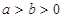 ),半焦距为
),半焦距为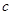 ,
,由
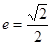 得,
得,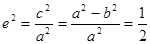 ,得
,得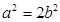 …………………………2分
…………………………2分由
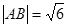 得,
得,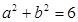 , ……………………………………………4分
, ……………………………………………4分故
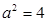 ,
,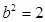
所以,椭圆
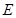 的方程为
的方程为 …………………………………………5分
…………………………………………5分(2)由
 ,消去
,消去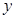 ,并整理得:
,并整理得: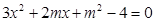 ,………7分
,………7分由判别式
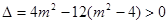 ,解得
,解得 ………………8分
………………8分设
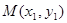 ,
,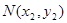 ,则
,则 ,
,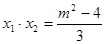 ……………10分
……………10分由
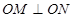 ,得
,得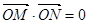 又
又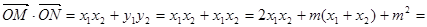
 ,故
,故 ………………………12分
………………………12分 点评:直线与椭圆的位置关系通常联立方程利用韦达定理求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是离心率为
是离心率为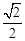 的椭圆,
的椭圆,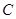 :
: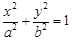 (
(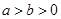 )的左、右焦点,直线
)的左、右焦点,直线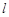 :
: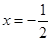 将线段
将线段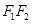 分成两段,其长度之比为1 : 3.设
分成两段,其长度之比为1 : 3.设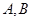 是
是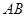 的中点
的中点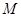 在直线
在直线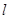 上,线段
上,线段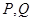 两点.
两点.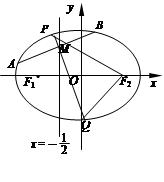
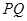 为直径的圆经过点
为直径的圆经过点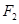 ,若存在,求出
,若存在,求出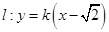 与双曲线
与双曲线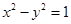 仅有一个公共点,则实数
仅有一个公共点,则实数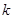 的值为
的值为 的焦距是( )
的焦距是( )


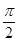 ,
,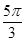 ),P2的柱坐标是P2(2,
),P2的柱坐标是P2(2,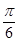 ,1),则|P1P2|=( )
,1),则|P1P2|=( )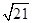

 轴上的抛物线过点
轴上的抛物线过点 .
. 作直线交抛物线于
作直线交抛物线于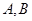 两点,使得
两点,使得 恰好平分线段
恰好平分线段 ,求直线
,求直线 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为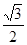 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为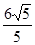 。
。
 的取值范围.
的取值范围.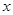 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线 对称.
对称. 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线 轴上的截距b的取值范围.
轴上的截距b的取值范围.