题目内容
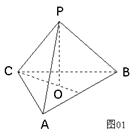
设S为 平面外的一点,SA=SB=SC,
平面外的一点,SA=SB=SC, ,若
,若 ,求证:平面ASC
,求证:平面ASC 平面ABC。
平面ABC。
 平面外的一点,SA=SB=SC,
平面外的一点,SA=SB=SC, ,若
,若 ,求证:平面ASC
,求证:平面ASC 平面ABC。
平面ABC。(1)把角的关系转化为边的关系
(2)利用棱锥的性质(三棱锥的侧棱相等,则顶点在底面上的射影为底面三角形的外心)
证明:设D为AB的中点

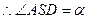

同理
 且
且

即 为
为 且S在平面上的射影O为
且S在平面上的射影O为 的外心
的外心
则O在斜边AC的中点。
 平面ABC
平面ABC
 平面SAC
平面SAC
 平面ASC
平面ASC 平面ABC
平面ABC
(2)利用棱锥的性质(三棱锥的侧棱相等,则顶点在底面上的射影为底面三角形的外心)
证明:设D为AB的中点

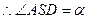

同理

 且
且

即
 为
为 且S在平面上的射影O为
且S在平面上的射影O为 的外心
的外心则O在斜边AC的中点。
 平面ABC
平面ABC 平面SAC
平面SAC 平面ASC
平面ASC 平面ABC
平面ABC
练习册系列答案
相关题目
 是平行四边形
是平行四边形 平面外一点,
平面外一点, 分别是
分别是 上的点,且
上的点,且 =
= , 求证:
, 求证: 平面
平面

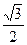 AB,E是AB的中点,G是△PCD的重心,则在平面PCD内过G点且与PE垂直的直线有( )
AB,E是AB的中点,G是△PCD的重心,则在平面PCD内过G点且与PE垂直的直线有( )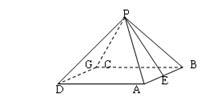

 中,
中, 是平面
是平面 上的线段,
上的线段, 平面
平面


 为直线,
为直线, 为平面,则下列命题中不正确的是( )
为平面,则下列命题中不正确的是( )


