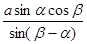题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的一段图象如下所示.
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.

| π |
| 2 |
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.

(1)由图象可以得到函数f(x)的振幅A=3,
设函数周期为T,则
T=4π-
=
,
所以T=5π,则ω=
=
=
,
由ωx0+Φ=0,得
×
+Φ=0,所以Φ=-
,
所以f(x)=3sin(
x-
).
(2)由
+2kπ≤
x-
≤
π+2kπ(k∈Z),
得
π+5kπ≤x≤4π+5kπ(k∈Z),
所以函数的减区间为(
π+5kπ,4π+5kπ)k∈Z.
函数f(x)的最大值为3,当且仅当
x-
=
+2kπ(k∈Z),
即x=
π+5kπ(k∈Z)时函数取得最大值.
所以函数的最大值为3,取得最大值时的x的集合为{x|x=
π+5kπk∈Z}.
设函数周期为T,则
| 3 |
| 4 |
| π |
| 4 |
| 15π |
| 4 |
所以T=5π,则ω=
| 2π |
| T |
| 2π |
| 5π |
| 2 |
| 5 |
由ωx0+Φ=0,得
| 2 |
| 5 |
| π |
| 4 |
| π |
| 10 |
所以f(x)=3sin(
| 2 |
| 5 |
| π |
| 10 |
(2)由
| π |
| 2 |
| 2 |
| 5 |
| π |
| 10 |
| 3 |
| 2 |
得
| 3 |
| 2 |
所以函数的减区间为(
| 3 |
| 2 |
函数f(x)的最大值为3,当且仅当
| 2 |
| 5 |
| π |
| 10 |
| π |
| 2 |
即x=
| 3 |
| 2 |
所以函数的最大值为3,取得最大值时的x的集合为{x|x=
| 3 |
| 2 |

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目


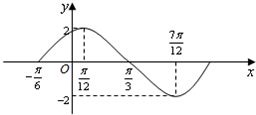

 (sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
(sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°, (cos80°-2cos250°+1),则a,b,c的大小关系是 ( ).
(cos80°-2cos250°+1),则a,b,c的大小关系是 ( ). ,从C,D两点测得A点仰角分别是
,从C,D两点测得A点仰角分别是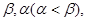 则A点离地面的高度等于( )
则A点离地面的高度等于( )