题目内容

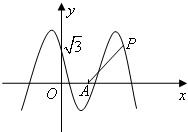
如图为函数y=Asin（ωx+φ）+c（A＞0，ω＞0，0＜φ＜2π）图象的一部分，
（1）求函数的解析式；
（2）此函数的图象可由函数y=sinx的图象经过怎样的变换而得？
（1）A=
4-(-2)
2
=3，c=
4+(-2)
2
=1
∵
3
4
T=8∴T=
32
3

即
2π
?
=
32
3
，?=
3π
16

∴y=3sin(
3π
16
x+ϕ)+1
∵（12，4）在函数图象上
∴4=3sin(
3π
16
•12+ϕ)+1，
即sin(
9π
4
+ϕ)=1
∴
9π
4
+ϕ=
π
2
+2kπ，k∈Z，得ϕ=-
7π
4
+2kπ，k∈Z
∴函数解析式为y=3sin(
3π
16
x+
π
4
)+1
（2）先将函数的图象向左平移
π
4
个单位，
然后横坐标不变，纵坐标变为原来的3倍，
再纵坐标不变，横坐标变为原来的
16
3π
倍，
最后向上平移1个单位．
练习册系列答案
相关题目
将函数y=2sin（2x-
π
3
）的图象向左平移
π
6
个单位所得图象的函数解析式为______．
将函数y=sin(x-
π
3
)，x∈[0，2π]的图象上各点的纵坐标不变横坐标伸长到原来的2倍，再向左平移
π
6
个单位，所得函数的单调递增区间为______．
y=sin（ωx+φ），ω＞0与y=a函数图象相交有相邻三点，从左到右为P、R、Q，若PR=3RQ，则a的值______．
将函数f（x）=cos2x的图象向右平移
π
4
个单位，得到函数y=g（x）的图象，则（　　）
A．g(x)=cos(2x-
π
4
)		B．g(x)=cos(2x+
π
4
)
C．g（x）=sin2xD．g（x）=-sin2x
定义在区间[-π，
2
3
π]上的函数y=f（x）的图象关于直线x=-
π
6
对称，当x∈[-
π
6
，
2
3
π]时，函数f（x）=Asin（ωx+φ），(A＞0，ω＞0，-
π
2
＜φ＜
π
2
)，其图象如图．
（Ⅰ）求函数y=f（x）在[-π，
2
3
π]上的表达式；
（Ⅱ）求方程f(x)=
2
2
的解集．
如图，函数y=2cos(ωx+θ)(x∈R，0≤θ≤
π
2
)的图象与y轴交于点(0，
3
)，且在该点处切线的斜率为-2．
（1）求θ和ω的值；
（2）已知点A(
π
2
，0)，点P是该函数图象上一点，点Q（x0，y0）是PA的中点，当y0=
3
2
，x0∈[
π
2
，π]时，求x0的值．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的一段图象如下所示．
（1）求f（x）的解析式；
（2）求f（x）的单调减区间，并指出f（x）的最大值及取到最大值时x的集合．
设α、β都是锐角且cosα＝，sin(α＋β)＝，则cosβ＝(　 　).
A．B．C．或D．或

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网