题目内容

若函数f（x）=sinωx+
3
cosωx（x∈R），又f（α）=-2，f（β）=0，且|α-β|的最小值为
3π
4
，则正数ω的值是（　　）
A．
3
2
B．
4
3
C．
2
3
D．
1
3
f（x）=2sin（ωx+
π
3
），
由f（α）=-2，得ωα+
π
3
=2k1π-
π
2
，k1∈Z，∴α=
2k1π
ω
-
5π
6ω
，
由f（β）=0，得ωβ+
π
3
=k2π，k2∈Z，∴β=
k2π
ω
-
π
3ω
，
则α-β=
2(k1-k2)π
ω
-
π
2ω
=
4(k1-k2)π-π
2ω
=
(4k-1)π
2ω
，k∈Z，
当k=0时|α-β|取得最小值
π
2ω
，则
π
2ω
=
3π
4
，解得ω=
2
3
，
故选C．
练习册系列答案
相关题目
将函数y=sinx的图象向右平移
π
2
个单位长度，再向上平移1个单位长度，所得的图象对应的函数解析式为（　　）
A．y=1-sinxB．y=1+sinxC．y=1-cosxD．y=1+cosx
将函数y=2sin（2x-
π
3
）的图象向左平移
π
6
个单位所得图象的函数解析式为______．
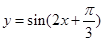将函数的图象按向量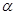平移后所得的图象关于点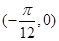中心对称，则向量的坐标可能为（   ）
A．B．C．D．
y=sin（ωx+φ），ω＞0与y=a函数图象相交有相邻三点，从左到右为P、R、Q，若PR=3RQ，则a的值______．
对于函数f（x）（x∈D），若存在两条距离为d的直线y=kx+m1和y=kx+m2，使任意x∈D都有kx+m1≤f（x）≤kx+m2恒成立，则称函数f（x）（x∈D）有一个宽度为d的通道．
下列函数：
①f(x)=
1
x
；
②f（x）=sinx；
③f(x)=
x2-1
；
④f（x）=x3+1．
其中[1，+∞）上通道宽度可以为1的函数的序号是______（填上所有正确答案的序号）
函数y=tan（
π
4
-2x）的一个减区间是（　　）
A．（0，
π
2
）		B．（-
5π
8
，
π
8
）		C．（-
3π
8
，
5π
8
）		D．（
3π
8
，
7π
8
）
将函数f（x）=cos2x的图象向右平移
π
4
个单位，得到函数y=g（x）的图象，则（　　）
A．g(x)=cos(2x-
π
4
)		B．g(x)=cos(2x+
π
4
)
C．g（x）=sin2xD．g（x）=-sin2x
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的一段图象如下所示．
（1）求f（x）的解析式；
（2）求f（x）的单调减区间，并指出f（x）的最大值及取到最大值时x的集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网