已知命题p:x＞k.命题q:$\frac{3}{x+1}$＜1,如果p是q的充分不必要条件.则k的取值范围是k≥2．题目和参考答案——青夏教育精英家教网——

题目内容

9．已知命题p：x＞k，命题q：$\frac{3}{x+1}$＜1；如果p是q的充分不必要条件，则k的取值范围是k≥2．

分析分别解出关于p，q的x的范围，结合充分必要条件的定义，从而求出k的范围．

解答解：由命题q：$\frac{3}{x+1}$＜1；解得：x＞2或x＜-1，
设集合A={x|x＞k}，B={x|x＞2或x＜-1}，
如果p是q的充分不必要条件，
则A?B，
∴k≥2，
故答案为：k≥2．

点评本题考查了充分必要条件，考查解不等式问题，是一道基础题．

练习册系列答案

中考211系列答案

寒假生活四川大学出版社系列答案

响叮当寒假作业广州出版社系列答案

无敌战卷课时作业系列答案

中考夺标全国各省市中考试题分类系列答案

星空小学假期作业寒假乐园新疆青少年出版社系列答案

快乐假期寒假作业延边教育出版社系列答案

寒假直通车河北美术出版社系列答案

华章教育寒假总复习学习总动员系列答案

学习报中考备战系列答案

相关题目

19．已知数列{a_n}满足：a₁=$\frac{1}{3}$，a_n+1=a_n²+a_n，用[x]表示不超过x的最大整数，如[2.6]=2，[-0.6]=-1，则 $[\frac{1}{{{a_1}+1}}+\frac{1}{{{a_2}+1}}+…+\frac{1}{{{a_{2015}}+1}}]$的值等于（　　）

20．已知函数f（x）=x²+2x+2（x≥-1），求f^-1（2）．

17．函数y=$\frac{\sqrt{4-{x}^{2}}}{x-1}$+（x+2）⁰的定义域为{x|-2＜x＜1或1＜x≤2}．

4．已知两个等差数列{a_n}、{b_n}，它们的前n项和分别是S_n、T_n，若$\frac{S_n}{T_n}$=$\frac{2n+3}{3n-1}$，则$\frac{{{a_3}+{a_5}}}{{{b_3}+{b_5}}}$+$\frac{a_4}{{{b_2}+{b_6}}}$=$\frac{51}{40}$．

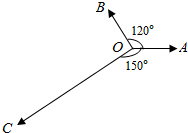如图所示，平面内有三个向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为120°，$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为150°，且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$，$|{\overrightarrow{OC}}|=2\sqrt{3}$，若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$（λ，μ∈R），则λ+μ=（　　）

1．已知椭圆E的中心在原点O，焦点在x轴上，离心率e=$\frac{\sqrt{2}}{2}$，原点O到椭圆E的右顶点与上顶点所在直线的距离为$\frac{2\sqrt{6}}{3}$．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若过椭圆E右焦点F的直线l与椭圆E相交于M，N两点（M，N均在y轴右侧），点A（0，2）、B（0，-2），设A，B，M，N四点构成的四边形的面积为S，求S的取值范围．

18．在△ABC中，A、B、C的对边分别为a、b、c，已知b=2$\sqrt{7}$，B=60°，a+c=10．
（1）求sin（A+30°）；
（2）若D为△ABC外接圆劣弧AC上的一点，且2AD=DC，求四边形ABCD的面积．

19．设f（x）=|lgx|，若函数g（x）=f（x）-ax在区间（0，4）上有三个零点，则实数a的取值范围是（　　）

$（{\frac{lg2}{2}，\frac{lge}{e}}）$

$（{0，\frac{1}{e}}）$

$（{\frac{lg2}{2}，e}）$

$（{0，\frac{lg2}{2}}）$