题目内容
1.已知椭圆E的中心在原点O,焦点在x轴上,离心率e=$\frac{\sqrt{2}}{2}$,原点O到椭圆E的右顶点与上顶点所在直线的距离为$\frac{2\sqrt{6}}{3}$.(Ⅰ)求椭圆E的方程;
(Ⅱ)若过椭圆E右焦点F的直线l与椭圆E相交于M,N两点(M,N均在y轴右侧),点A(0,2)、B(0,-2),设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
分析 (1)根据题意,设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),由题意可得$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$与$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=$\frac{8}{3}$;联立两个式子,解可得a2与b2的值,代入椭圆的方程可得答案;
(2)由(Ⅰ)可得,A、B恰好是椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1的上下两个端点,如图,连接OM、ON,设直线MN方程为x=my+2,结合图形可得-1<m<1,联立$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,消去x,得(m2+2)y2+4my-4=0,由韦达定理可得|y1-y2|的表达式,又由于S=S△OAM+S△OBN+S△OMN,可以将S用m表示出来,令t=m2+1,则1≤t<2,则S=$\frac{4\sqrt{2}t+8}{{t}^{2}+1}$,
对S求导可得S′<0,可得面积函数在[1,2)上单调递减,结合t的范围即可得S的范围.
解答  解:(Ⅰ)根据题意,设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
解:(Ⅰ)根据题意,设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
则c=$\sqrt{{a}^{2}-{b}^{2}}$,有e=$\frac{\sqrt{2}}{2}$,则$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,①
又由于原点O到椭圆E的右顶点与上顶点所在直线的距离为$\frac{2\sqrt{6}}{3}$,则有$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=$\frac{8}{3}$,②
联立①②可得:a2=8,b2=4,
则椭圆的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1,
(Ⅱ)由(Ⅰ)可得,A、B恰好是椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1的上下两个端点,点M(x1,y1),N(x2,y2),
如图,连接OM、ON,设直线MN方程为x=my+2,
由于M,N均在y轴右侧,则有KAF<m<KBF,即-1<m<1,
联立$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,消去x,得(m2+2)y2+4my-4=0,
则y1+y2=$\frac{4m}{{m}^{2}+2}$,y1y2=-$\frac{4}{{m}^{2}+2}$,
则|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(\frac{4m}{{m}^{2}+2})^{2}+\frac{16}{{m}^{2}+2}}$=$\frac{4\sqrt{2}\sqrt{{m}^{2}+1}}{{m}^{2}+2}$;
由于M,N均在y轴右侧,则x1>0,x2>0,
则S=S△OAM+S△OBN+S△OMN=$\frac{1}{2}$×2(x1+x2)+$\frac{1}{2}$×2|y1-y2|=m(y1+y2)+4+|y1-y2|
=-$\frac{4{m}^{2}}{{m}^{2}+2}$+4+$\frac{4\sqrt{2}\sqrt{{m}^{2}+1}}{{m}^{2}+2}$=$\frac{4\sqrt{2}\sqrt{{m}^{2}+1}+8}{{m}^{2}+2}$,
即S=$\frac{4\sqrt{2}\sqrt{{m}^{2}+1}+8}{{m}^{2}+2}$,令t=m2+1,则1≤t<2,则S=$\frac{4\sqrt{2}t+8}{{t}^{2}+1}$,
则S′=$\frac{-4\sqrt{2}{t}^{2}-16t+4\sqrt{2}}{({t}^{2}+1)^{2}}$=-$\frac{4\sqrt{2}({t}^{2}+2\sqrt{2}t-1)}{({t}^{2}+1)^{2}}$<0,故面积函数在[1,2)单调递减,
又由1≤t<2,则$\frac{16}{3}$<S≤2$\sqrt{2}$+4,
所以所以面积S的取值范围是($\frac{16}{3}$,2$\sqrt{2}$+4].
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、三角形的面积计算公式、利用导数研究函数的单调性、基本不等式的性质,考查了推理能力与计算能力.

| A. | 43 | B. | $A_4^3$ | C. | $C_4^3$ | D. | 4 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
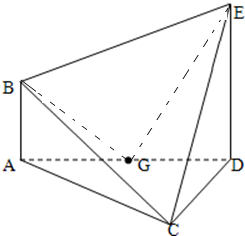 在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.
在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.