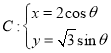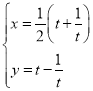题目内容
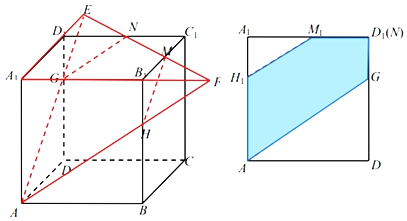
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
【答案】![]()
【解析】
由图象可得投影为五边形AH1M1D1G,利用三角形相似性质得到DG=2D1G![]() ,BH=2B1H
,BH=2B1H![]() ,进而求得AH1=2A1H1
,进而求得AH1=2A1H1![]() ,A1M1=D1M1
,A1M1=D1M1![]() ,则可得
,则可得![]() 1
1![]() SADG.
SADG.
解:直线MN分别与直线A1D1,A1B1交于E,F两点,
连接AE,AF,分别与棱DD1,BB1交于G,H两点,连接GN,MH,
得到截面五边形AGNMH,
向平面ADD1A1作投影,得到五边形AH1M1D1G,
由点M,N分别是棱B1C1,C1D1的中点,可得D1E=D1N![]() ,
,
由△D1EG∽△DAG,可得DG=2D1G![]() ,
,
同理BH=2B1H![]() ,
,
则AH1=2A1H1![]() ,A1M1=D1M1
,A1M1=D1M1![]() ,
,
则![]() 1
1![]() SADG=1
SADG=1![]() 1
1![]() ,
,

故答案为:![]() .
.

练习册系列答案
相关题目