题目内容
16．设集合A={x|x2-1＜0}，B={x|x+2≥0}，则A∩B=（ ）| A． | {x|-1＜x＜1} | B． | {x|x≥-2} | C． | {x|-2≤x＜1} | D． | {x|-1＜x≤2} |
分析 分别求出A与B中不等式的解集确定出A与B，找出A与B的交集即可．
解答 解：由A中不等式变形得：（x+1）（x-1）＜0，
解得：-1＜x＜1，即A={x|-1＜x＜1}，
由B中不等式解得：x≥-2，即B={x|x≥-2}，
则A∩B={x|-1＜x＜1}，
故选：A．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
6．
将正奇数组成的数列{an}，按下表排成5列：
（Ⅰ）求第五行到第十行的所有数的和；
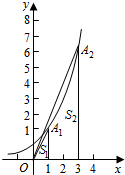
（Ⅱ）已知点A1（a1，b1），A2（a2，b2），…，An（an，bn）在指数函数y=2x的图象上，如果，以A1，A2，…，An为一个顶点，x轴y轴为邻边构成的矩形面积为S1，S2，…Sn，求S1+S2+…+Sn的值Tn．
将正奇数组成的数列{an}，按下表排成5列：| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
（Ⅱ）已知点A1（a1，b1），A2（a2，b2），…，An（an，bn）在指数函数y=2x的图象上，如果，以A1，A2，…，An为一个顶点，x轴y轴为邻边构成的矩形面积为S1，S2，…Sn，求S1+S2+…+Sn的值Tn．
7．已知四面体ABCD的所有顶点都在球O的球面上，球O的半径为2，AB，AC，AD两两垂直，AB=$\sqrt{2}$，则四面体ABCD体积的最大值为（ ）
| A． | $\frac{7\sqrt{2}}{6}$ | B． | $\frac{7}{3}$ | C． | 2$\sqrt{2}$ | D． | 2 |
4．设函数f（x）=$\frac{1}{2}$cosωx对任意的x∈R，都有f（$\frac{π}{6}$-x）=f（$\frac{π}{6}$+x），若函数g（x）=-2+3sinωx，则g（$\frac{π}{6}$）的值是（ ）
| A． | 1 | B． | -5或3 | C． | -2 | D． | $\frac{1}{2}$ |
5．在复平面内，复数$\frac{2i}{1-i}$对应的点的坐标是（ ）
| A． | （-1，1） | B． | （-1，-1） | C． | （1，-1） | D． | （1，1） |