题目内容
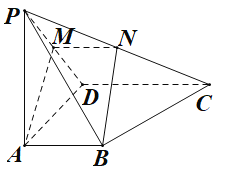
【题目】在三棱锥
中，
底面
，
，
是线段
上一点，且
.三棱锥的各个顶点都在球
表面上，过点作球的截面，若所得截面圆的面积的最大值与最小值之差为
，则球的表面积为（ ）
A.
B.
C.
D.
【答案】C
【解析】
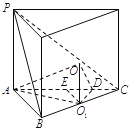
将三棱锥
补成直三棱柱，根据球的性质，确定球心位置，要使过点
作球
的截面圆的面积最小，只需截面与
垂直，当截面过球心时，截面面积最大，即可求解.
将三棱锥补成直三棱柱，
且三棱锥和该直三棱柱的外接球都是球，
记三角形
的中心为
，设球的半径为
，
，
则球心到平面的距离为
，即
，
连接
，则
，∴
.
在
中，取
的中点为
，连接
，
则
，
，
所以
.在
中，
，
由题意得到当截面与直线垂直时，截面面积最小，
设此时截面圆的半径为
，
则
，
所以最小截面圆的面积为
，
当截面过球心时，截面面积最大为
，
所以
，
，
球的表面积为
.
故选:C.
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
