题目内容
19.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow a$的夹角为$\frac{π}{6}$,向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow b$的夹角为$\frac{π}{4}$则$\frac{|\overrightarrow a|}{|\overrightarrow b|}$等于$\sqrt{2}$.分析 根据题意画出?ABCD,设$\overrightarrow{AB}=\overrightarrow{a}$、$\overrightarrow{AD}=\overrightarrow{b}$,根据平行四边形法则求出$\overrightarrow{a}+\overrightarrow{b}$,由题意求出∠DAC、∠CAB和∠ACD,利用正弦定理求出$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$的值.
解答 解:由题意画出?ABCD,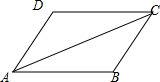 设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AD}=\overrightarrow{b}$,则$\overrightarrow{a}+\overrightarrow{b}$=$\overrightarrow{AC}$,
设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AD}=\overrightarrow{b}$,则$\overrightarrow{a}+\overrightarrow{b}$=$\overrightarrow{AC}$,
∵向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow a$的夹角为$\frac{π}{4}$,向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow b$的夹角为$\frac{π}{4}$,
∴∠DAC=$\frac{π}{4}$,∠CAB=$\frac{π}{6}$,则∠ACD=$\frac{π}{6}$,
在△ADC中,由正弦定理得$\frac{CD}{sin∠DAC}=\frac{AD}{sin∠ACD}$,
∴$\frac{CD}{AD}=\frac{sin∠DAC}{sin∠ACD}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=$\sqrt{2}$,则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查向量的加法法则,以及其几何意义,以及正弦定理的应用,考查数形结合思想.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | 4 | B. | 6 | C. | 10 | D. | 无法确定 |
