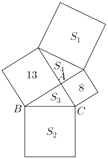
题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() ,
,
(1)当![]() 时,求使得等式
时,求使得等式![]() 成立的
成立的![]() 的取值范围;
的取值范围;
(2)当![]() 时,求使得等式
时,求使得等式![]() 成立的
成立的![]() 的取值范围;
的取值范围;
(3)求![]() 的区间
的区间![]() 上的最大值
上的最大值![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 得
得![]() ,再将
,再将![]() 代入不等式得:
代入不等式得:![]() ,对
,对![]() 进行讨论去绝对值,从而得到
进行讨论去绝对值,从而得到![]() 的取值范围;
的取值范围;
(2)问题等价于解不等式![]() ,其中
,其中![]() ,对
,对![]() 分成
分成![]() 和
和![]() 两种情况去掉绝对值,再解含参不等式;
两种情况去掉绝对值,再解含参不等式;
(3)由题意得![]() 为一个分段函数,利用(2)的结论得
为一个分段函数,利用(2)的结论得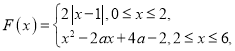 分别求出每一段函数的最大值,再进行比较,最大的即为函数
分别求出每一段函数的最大值,再进行比较,最大的即为函数![]() 的最大值.
的最大值.
(1)由![]() 得
得![]() ,
,
因为![]() ,所以上述不等式等价于
,所以上述不等式等价于![]() ①,
①,
当![]() 时,①
时,①![]() ,解得:
,解得:![]() ,所以
,所以![]() ;
;
当![]() 时,①
时,①![]() ,方程无解,所以
,方程无解,所以![]() ;
;
综上所述![]() .
.
(2)因为![]() ,所以
,所以![]()
由![]() ,当
,当![]() 时,
时,
![]() 显然成立,
显然成立,
所以![]() 不成立.
不成立.
当![]() 时,
时,![]() ,
,
方程的两根为![]() ,且
,且![]() ,
,
所以![]() 的解为
的解为![]() ,与
,与![]() 取交集还是
取交集还是![]() ,
,
综上所述:使![]() 成立的
成立的![]() 的取值范围是
的取值范围是![]() .
.
(3)由(2)得,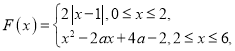
当![]() 时,
时,![]() ,此时,
,此时,![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() 的最大值为
的最大值为![]() 中较大者,
中较大者,
当![]() 时,即
时,即![]() ,
,![]() ;
;
当![]() 时,即
时,即![]() ,
,![]() ;
;
当![]() 时,即
时,即![]() ,
,![]() ;
;
所以![]()
综上所述:![]()

练习册系列答案
相关题目