Question

【题目】已知数列各项不为0，前项和为.

（1）若，，求数列的通项公式；

（2）在（1）的条件下，已知，分别求和的表达式；

（3）证明：是等差数列的充要条件是：对任意，都有：.

Answer 1

【答案】（1）；（2） 4（）n﹣4，；（3）证明见解析

【解析】

根据与的关系式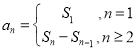， ，计算即可得出答案.

（2）将各项配凑成二项式展开式的形式，再利用二项式展开式的性质计算即可;关于，利用倒序求和法，再用二项式展开式化简，即可得出答案.

（3）必要性：利用裂项相消法化简即可得证；充分性：两次作差变形即可说明其为等差数列.

（1） 因为，所以

当时，

当时，有

即

所以数列为以为首项，为公比的等比数列.

所以.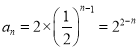

（2），

所以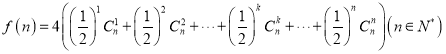

所以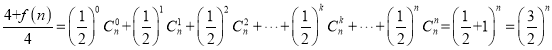

所以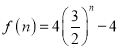

①

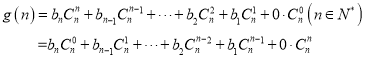②

①+②：

（3）证明：先证必要性.设数列的公差为,若，则不等式显然成立.

若，则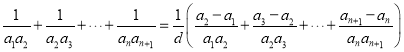

.

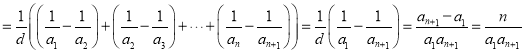再证充分性：依题意有，

，

化简得：

同理可得：

得：，即.

所以数列为等差数列.