题目内容
20.如图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的体积为(2+$\frac{\sqrt{3}}{3}$)π.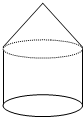
分析 分别计算圆锥和圆柱的体积,即可得出结论.
解答 解:由题意,圆锥的高为$\sqrt{3}$,体积为$\frac{1}{3}π•{1}^{2}•\sqrt{3}$=$\frac{\sqrt{3}}{3}$π,
圆柱的体积为π•12•2=2π,
∴该组合体的体积为(2+$\frac{\sqrt{3}}{3}$)π.
故答案为:(2+$\frac{\sqrt{3}}{3}$)π.
点评 本题考查圆锥和圆柱的体积,考查学生的计算能力,比较基础.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
11.(2x+1)5(x2-$\frac{2}{x}$+$\frac{1}{{x}^{4}}$)的展开式的常数项是( )
| A. | 100 | B. | -100 | C. | 60 | D. | -60 |
9.已知全集U=R,A={x|x<1},B={y|-|x|+y=2},则集合∁U(A∪B)=( )
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
10.若复数Z满足$\overline Z$(1+i)=2i,则在复平面内Z对应的点的坐标是( )
| A. | (1,1) | B. | (1,-l) | C. | (-l,1) | D. | (-l,-l) |
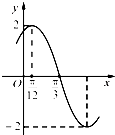 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )