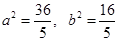题目内容
长短轴之比为三比二,一个焦点是(0.-2) 中心在原点的椭圆方程是

:∵中心在原点, 一个焦点是(0,-2),
则椭圆的标准方程为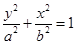
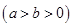 且c=2
且c=2
又∵长短轴之比为3∶2, ∴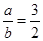 ………①
………①
而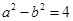 ………② 由①②得
………② 由①②得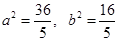
故椭圆的标准方程为
则椭圆的标准方程为
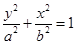
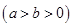 且c=2
且c=2又∵长短轴之比为3∶2, ∴
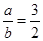 ………①
………①而
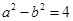 ………② 由①②得
………② 由①②得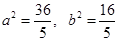
故椭圆的标准方程为


练习册系列答案
相关题目
题目内容

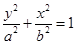
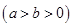 且c=2
且c=2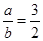 ………①
………①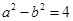 ………② 由①②得
………② 由①②得