题目内容
已知曲线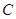 :
: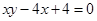 ,数列
,数列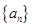 的首项
的首项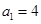 ,且
,且
当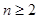 时,点
时,点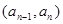 恒在曲线
恒在曲线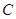 上,数列{
上,数列{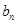 }满足
}满足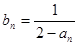
(1)试判断数列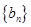 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列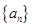 和
和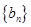 的通项公式;
的通项公式;
(3)设数列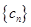 满足
满足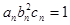 ,试比较数列
,试比较数列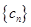 的前
的前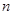 项和
项和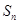 与
与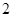 的大小.
的大小.
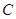 :
: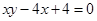 ,数列
,数列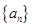 的首项
的首项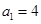 ,且
,且当
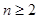 时,点
时,点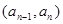 恒在曲线
恒在曲线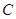 上,数列{
上,数列{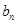 }满足
}满足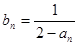
(1)试判断数列
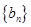 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;(2)求数列
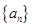 和
和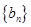 的通项公式;
的通项公式;(3)设数列
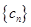 满足
满足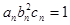 ,试比较数列
,试比较数列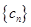 的前
的前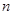 项和
项和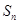 与
与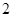 的大小.
的大小.(1)数列{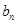 }是公差为
}是公差为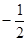 的等差数列
的等差数列
(2)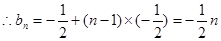 ,
,
(3)根据通项公式的特点,采用裂项法来求和,并能比较大小。
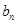 }是公差为
}是公差为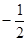 的等差数列
的等差数列(2)
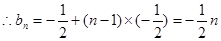 ,
,
(3)根据通项公式的特点,采用裂项法来求和,并能比较大小。
试题分析:解;(1)∵当
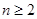 时,点
时,点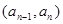 恒在曲线C上
恒在曲线C上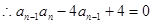 1分
1分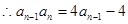
由
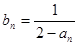 得
得当
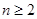 时,
时,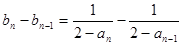
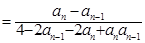
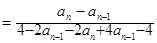
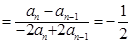 5分
5分∴数列{
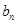 }是公差为
}是公差为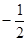 的等差数列. 6分
的等差数列. 6分(2)
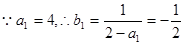
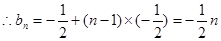 8分
8分由
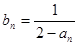 得
得 10分
10分(3)
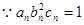
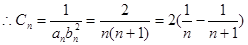 12分
12分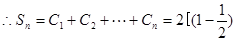
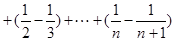 ]
]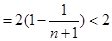
14分
点评:解决的关键是利用数列的概念以及裂项法求和进而比较大小,属于基础题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 ,
, 是等差数列,则数列
是等差数列,则数列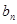 =
=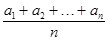
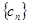 是等比数列,且
是等比数列,且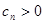 ,
, 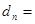 ____________
____________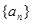 是单调递增的等差数列,首项
是单调递增的等差数列,首项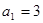 ,前
,前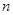 项和为
项和为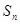 ,数列
,数列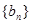 是等比数列,首项
是等比数列,首项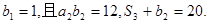
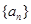 和
和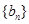 的通项公式.
的通项公式.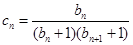 ,数列
,数列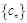 的前
的前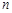 项和为
项和为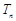 ,求证:
,求证: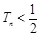 .
.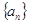 的首项为1,其前n项和为
的首项为1,其前n项和为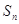 ,
,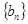 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为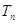 . 若
. 若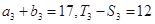 .
.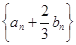 的前n项和
的前n项和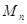 .(5分)
.(5分) 的前3项和
的前3项和 且
且 ,则
,则 等于( )
等于( ) .
. , an=2n+1,则a3= ( )
, an=2n+1,则a3= ( )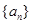 、
、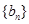 的前项和分别为
的前项和分别为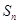 、
、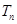 ,对任意的
,对任意的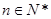 都有
都有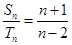 ,则
,则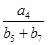
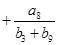 = .
= .