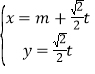题目内容
【题目】设奇函数
在（0，+∞）上为单调递增函数，且
，则不等式
的解集为 。
【答案】
【解析】
首先根据f（x）在（0，+∞）上为单调递增函数，且f（2）＝0，得到当0＜x＜2时，f（x）＜0；当x≥2时，f（x）≥0．再结合函数为奇函数证出：当x≤﹣2时，f（x）≤0且﹣2＜x＜0时，f（x）＞0，最后利用这个结论，将原不等式变形，讨论可得所求解集．
∵f（x）在（0，+∞）上为单调递增函数，且f（2）＝0，
∴当0＜x＜2时，f（x）＜0；当x≥2时，f（x）≥0
又∵f（x）是奇函数
∴当x≤﹣2时，﹣x≥2，可得f（﹣x）≥0，从而f（x）＝﹣f（﹣x）＜0．即x≤﹣2时f（x）≤0；
同理，可得当﹣2＜x＜0时，f（x）＞0．
不等式
0可化为：
0，即
0
∴
或
，解之可得x≥2或x≤﹣2
所以不等式0的解集为
故答案为：
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】为测试特斯拉汽车的百米加速时间，研发人员记录了汽车在
取
、
、
、
、
、
、
时刻的位移，并对数据做了初步处理，得到图
.同时，令
，得到数据图
，现画出
与，与
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|
（1）根据散点图判断，与，与哪两个量之间线性相关程度更强？（直接给出判断即可）；
（2）根据（1）的结果选择线性相关程度更强的两个量，建立相应的回归直线方程；
（3）根据（2）的结果预计特斯拉汽车百米加速需要的时间.
附：对于一组数据
、
、
、
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.