题目内容
【题目】已知函数f（x）=|ax2+x﹣4a|，其中x∈[﹣2，2]，a∈[﹣1，1]．
（1）当α=1时，求函数y=f（x）的值域；
（2）记f（x）的最大值为M（a），求M（a）的取值范围．
【答案】
（1）解：当α=1时，f（x）=|x2+x﹣4|，x∈[﹣2，2]，
由x2+x﹣4=0，解得x= 
，
由f（x）在[﹣2，﹣ 
]递增，在（﹣ ， 
）递减，
在（ ，2]递增，可得
f（x）的最小值为0，由f（﹣ ）= 
，f（2）=4，
最大值为 ．
则f（x）的值域为[0， ]；
（2）解：设f（x）=0的两根为x1，x2，（x1＜x2），
当﹣1≤a≤﹣ 
时，f（x）在（﹣2，x1）递减，（x1，﹣ 
）递增，（﹣ ，2）递减，
可得f（x）在x=﹣ 处取得最大值，且为﹣ 
；
当﹣ ＜a≤0时，f（x）在（﹣2，x1）递减，（x1，2）递增，
可得f（x）在x=±2处取得最大值2；
当0＜a≤ 时，f（x）在（﹣2，x2）递减，（x2，2）递增，可得f（x）在x=±2处取得最大值2；
当 ＜a≤1时，f（x）在（﹣2，﹣ ）递增，（﹣ ，x2）递减，（x2，2）递增，
可得f（x）在x=﹣ 处取得最大值，且为 ．
即有M（a）=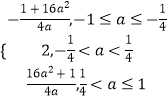 
，
当﹣1≤a≤﹣ 时，M（a）=（﹣4a）+ 
在[﹣1，﹣ ]递减，可得M（a）∈[2， ]；
当 ＜a≤1时，M（a）=4a+ 
递增，可得M（a）∈[2， ]．
综上可得，M（a）的取值范围是[2， ]
【解析】（1）求出当α=1时，f（x）=|x2+x﹣4|，x∈[﹣2，2]，解方程可得两根，再由f（x）的单调性，可得值域；（2）设f（x）=0的两根为x1 ， x2 ， （x1＜x2），对a讨论，当﹣1≤a≤﹣ 时，当﹣ ＜a≤0时，当0＜a≤ 时，当 ＜a≤1时，运用单调性可得最大值，再由基本不等式和单调性，即可得到所求范围．
【考点精析】掌握二次函数的性质和绝对值不等式的解法是解答本题的根本，需要知道当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减；含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．
