题目内容

5．若不等式ax2+bx-1＜0的解集为{x|-1＜x＜2}，则a+b=（　　）
A．6B．4C．2D．0

分析 不等式ax2+bx-1＜0的解集是{x|-1＜x＜2}，故-1，2是方程ax2+bx-1=0的两个根，由根与系数的关系求出a，b．

解答 解：由题意不等式ax2+bx-1＜0的解集是{x|-1＜x＜2}，故-1，2是方程ax2+bx-1=0的两个根，
∴-1+2=-$\frac{b}{a}$，-1×2=-$\frac{1}{a}$
∴a=$\frac{1}{2}$，b=$-\frac{1}{2}$
∴a+b=0
故选：D．

点评 本题考查一元二次不等式与一元二次方程的关系，解答本题的关键是根据不等式的解集得出不等式相应方程的根，再由根与系数的关系求参数的值．注意总结方程，函数，不等式三者之间的联系．

练习册系列答案
相关题目
15．已知A（5，-3），B（-1，3），点C在线段AB上，且$\frac{CB}{AB}$=$\frac{1}{3}$，则点C坐标是（1，1）．
16．已知向量$\overrightarrow{a}$=（2，m），$\overrightarrow{b}$=（-3，4），$\overrightarrow{c}$=（2m+7，3）（m∈R）．
（1）若$\overrightarrow{a}$∥$\overrightarrow{b}$，求实数m的值；
（2）若$\overrightarrow{a}$⊥$\overrightarrow{c}$，求（$\overrightarrow{a}$+$\overrightarrow{c}$）•$\overrightarrow{b}$的值．
13．已知f（x）=mx-lnx（0＜x≤e），g（x）=$\frac{lnx}{x}$，其中e是自然对数的底数，m∈R．
（1）当m=1时，求函数f（x）的单调区间和极值；
（2）求证：当m=1时，f（x）＞g（x）+1-$\frac{1}{e}$；
（3）是否存在实数m，使f（x）的最小值是2？若存在，求出m的值；若不存在，请说明理由．
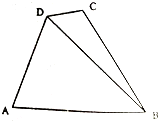20．随州市某处有如图所示的A、B、C、D四个景点，目前AD、AB、DC之间已修建公路，市政府为了更好发展随州的旅游产业，决定新修建两条公路用以连接B、D两景点和B、C两景点．现测得AD=5km，AB=7km，∠ADB=60°，∠ADC=105°，∠CBD=15°
（Ⅰ）求公路BD的长度；
（Ⅱ）求公路BC的长度．
10．已知关于x的方程（n+1）x2+mx-$\frac{n-1}{4}$=0（m，n∈R+）没有实数根，则关于x的方程4x2-4x+m+n=0有实数根的概率是（　　）
A．$\frac{2}{7π}$B．$\frac{2}{5π}$C．$\frac{2}{3π}$D．$\frac{2}{π}$
17．若函数f（x）=2|sinx|+sinx，（x∈[0，2π]）的图象与直线y=k有且仅有四个不同的交点，则k的取值范围是（0，1）．
14．已知向量$\overrightarrow a=（{1，-1}）$，$\overrightarrow b=（{1，2}）$，向量$\overrightarrow c$满足$（{\overrightarrow c+\overrightarrow b}）⊥\overrightarrow a$，$（{\overrightarrow c-\overrightarrow a}）∥\overrightarrow b$，则$\overrightarrow c$等于（　　）
A．（1，0）B．（2，1）C．（0，-1）D．$（{\frac{3}{2}，\frac{1}{2}}）$
15．已知向量$\vec a=（1，m），\vec b=（1，-3）$，且满足$（2\vec a+\vec b）⊥\vec b$
（Ⅰ）求向量$\vec a$的坐标及|$\overrightarrow{a}$+$\overrightarrow{b}$|；
（Ⅱ）求向量$\vec a$与$\vec b$的夹角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网