题目内容
15.已知集合A={x||x-2|>1},B={x|x2+px+q>0},若A=B,则p+q=( )| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
分析 通过解不等式求得集合A={x|x<1或x>3}.结合限制性条件A=B可以求得p、q的值,然后来求p+q的值.
解答 解:解不等式|x-2|>1得:x<1或x>3,即A={x|x<1或x>3}.
∵B={x|x2+px+q>0},A=B,
∴x1=1,x2=3是方程x2+px+q=0的两个根,
∴1+3=-p,1×3=q,即p=-4,q=3,
则p+q=-4+3=-1.
故选:B.
点评 本题考查集合相等的概念,解答的突破口是得到x1=1,x2=3是方程x2+px+q=0的两个根.

练习册系列答案
相关题目
5.通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如下表所示:
参考公式:$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程$\widehat{y}$=bx+a;
(3)现投入资金10(万元),求估计获得的利润为多少万元.
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程$\widehat{y}$=bx+a;
(3)现投入资金10(万元),求估计获得的利润为多少万元.
6.在中学综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
表2:女生
(1)从表2的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$临界值表
表1:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
5.某学校开展一次研究活动,获得的一组实验数据如表示数:
得到的回归方程为$\widehat{y}$=bx+a,则有( )
| x | 1 | 2 | 3 | 4 |
| y | 17 | 12 | 7 | 4 |
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b>0 | D. | a<0,b>0 |
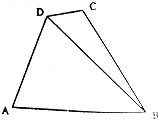 随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°
随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°