题目内容

17．实数x，y满足不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤0}\\{y≥-2}\end{array}\right.$，则目标函数z=x+3y的最小值是（　　）
A．-12B．-8C．-4D．0

分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．

解答 解：由约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤0}\\{y≥-2}\end{array}\right.$作出可行域如图，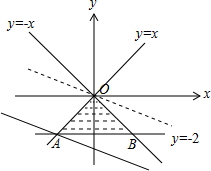

化目标函数z=x+3y为$y=-\frac{1}{3}x+\frac{z}{3}$，
由图可知，当直线$y=-\frac{1}{3}x+\frac{z}{3}$过A（-2，2）时，直线在y轴上的截距最小，z有最小值为-8．
故选：B．

点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．

练习册系列答案
相关题目
7．如图所示，已知A1B1C1-ABC是正棱柱，D是AC的中点，AB1⊥BC1，求二面角D-BC1-C的度数．
8．若直线y=kx+1与圆x2+y2=1相交于P、Q两点，且∠POQ=90°（其中O为原点），则k的值为（　　）
A．$\sqrt{2}$B．1C．$-\sqrt{2}$或$\sqrt{2}$D．-1或1
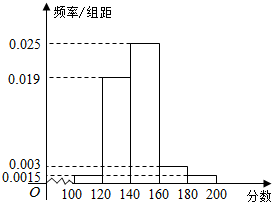5．某校为选拔参加“央视猜灯谜大赛”的队员，在校内组织猜灯谜竞赛．规定：第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛．现有200名学生参加知识测试，并将所有测试成绩绘制成如下所示的频率分布直方图．
（Ⅰ）估算这200名学生测试成绩的中位数，并求进入第二阶段比赛的学生人数；
（Ⅱ）将进入第二阶段的学生分成若干队进行比赛．现甲、乙两队在比赛中均已获得120分，进入最后抢答阶段．抢答规则：抢到的队每次需猜3条谜语，猜对1条得20分，猜错1条扣20分．根据经验，甲队猜对每条谜语的概率均为$\frac{3}{4}$，乙队猜对前两条的概率均为$\frac{4}{5}$，猜对第3条的概率为$\frac{1}{2}$．若这两队抢到答题的机会均等，您做为场外观众想支持这两队中的优胜队，会把支持票投给哪队？
12．已知数列{an}满足a1=10，an=$\left\{\begin{array}{l}{{2}^{{a}_{n-1}}，n=2k}\\{-1+lo{g}_{2}{a}_{n-1}，n=2k+1}\end{array}\right.$（n∈N*），其前n项和为Sn．
（Ⅰ）写出a3，a4；
（Ⅱ）求数列的通项公式；
（Ⅲ）求Sn的最大值．
2．一个四棱锥的三视图如图所示，则这个四棱锥的体积为$\frac{2}{3}$；表面积为3+$\sqrt{5}$．
9．如图，在矩形ABCD中，AB=2AD，M为CD的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．点O是线段AM的中点．

（Ⅰ）求证：平面DOB⊥平面ABCM；
（Ⅱ）求证：AD⊥BM；
（Ⅲ）过D点是否存在一条直线l，同时满足以下两个条件：
①l?平面BCD；②l∥AM．请说明理由．
6．为了解学生课外阅读的情况，随机统计了n名学生的课外阅读时间，所得数据都在[50，150]中，其频率分布直方图如图所示．已知在[50，75）中的频数为100，则n的值为1000．
7．已知集合A={-1，1}，B={x|x＜a}，若A∩B=∅，则（　　）
A．a≤-1B．a≥-1C．a≤1D．a＞1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网