题目内容
9.如图,在矩形ABCD中,AB=2AD,M为CD的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.点O是线段AM的中点.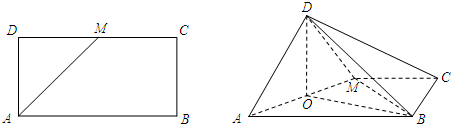
(Ⅰ)求证:平面DOB⊥平面ABCM;
(Ⅱ)求证:AD⊥BM;
(Ⅲ)过D点是否存在一条直线l,同时满足以下两个条件:
①l?平面BCD;②l∥AM.请说明理由.
分析 (Ⅰ)根据面面垂直的判定定理进行判断即可证明平面DOB⊥平面ABCM;
(Ⅱ)根据线面垂直的性质定理即可证明AD⊥BM;
(Ⅲ)利用反证法结合线面平行的性质进行证明.
解答 证明:(Ⅰ)由已知DA=DM,O是AM的中点,
∴DO⊥AM,
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,
DO?平面DOB,
∴平面DOB⊥平面ABCM;
(Ⅱ)在矩形ABCD中,AB=2AD,M为CD的中点,
∴AM=BM=$\sqrt{2}$AD=$\frac{\sqrt{2}}{2}$AB,
∴AM⊥BM,
由(1)知,DO⊥平面ABCM;
∵BM?平面ABCM,
∴DO⊥BM,
∵DO,AM?平面ADM,DO∩AM=0,
∴BM⊥平面ADM,
而AD?平面ADM,
∴AD⊥BM;
(Ⅲ)过D点是不存在一条直线l,同时满足以下两个条件:
①l?平面BCD;②l∥AM.
证明(反证法)
假设过D存在一条直线l满足条件,
则∵l∥AM,L?平面ABCM,AM?平面ABCM,
∴l∥平面ABCM,
∵l?平面BCD,平面ABCM∩平面BCD=BC,
∴l∥BC,
即AM∥BC,
由图易知,AM,BC相交,此时矛盾,
∴过D点不存在一条直线l满足题设条件.
点评 本题主要考查空间直线和平面平行,垂直以及面面垂直的判定,利用相应的判定定理是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目