题目内容
已知F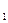 、F
、F 为双曲线
为双曲线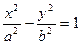 (a>0,b>0)的焦点,过F
(a>0,b>0)的焦点,过F 作垂直于x轴的直线交双曲线于点P,且∠PF
作垂直于x轴的直线交双曲线于点P,且∠PF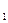 F
F =30
=30 ,求双曲线的渐近线方程。
,求双曲线的渐近线方程。
 、F
、F 为双曲线
为双曲线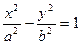 (a>0,b>0)的焦点,过F
(a>0,b>0)的焦点,过F 作垂直于x轴的直线交双曲线于点P,且∠PF
作垂直于x轴的直线交双曲线于点P,且∠PF F
F =30
=30 ,求双曲线的渐近线方程。
,求双曲线的渐近线方程。双曲线的渐近线方程为y=±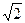 x
x
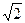 x
x设F (c,0)(c>0),P(c,y
(c,0)(c>0),P(c,y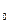 ),则
),则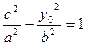 ,解得y
,解得y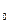 =±
=±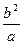 。
。
∴|P F |=
|=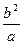 。
。
又∵在直角三角形P F F
F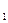 中,∠PF
中,∠PF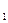 F
F =30
=30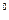
解法一:|F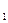 F
F |=
|=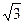 |P F
|P F |,即2c=
|,即2c=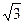
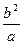 将c
将c =a
=a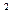 +b
+b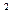 代入,解得b
代入,解得b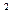 ="2" a
="2" a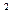
解法二:|PF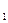 |="2|P" F
|="2|P" F |,由双曲线定义可知,|PF
|,由双曲线定义可知,|PF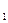 |-|P F
|-|P F |=2a,得|P F
|=2a,得|P F |=2a
|=2a
∵|P F |=
|=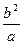 ,∴2a=
,∴2a=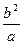 ,即b
,即b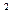 ="2" a
="2" a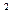 ∴
∴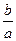 =
=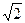
故所求双曲线的渐近线方程为y=±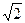 x 。
x 。
 (c,0)(c>0),P(c,y
(c,0)(c>0),P(c,y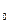 ),则
),则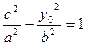 ,解得y
,解得y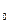 =±
=±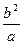 。
。∴|P F
 |=
|=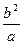 。
。又∵在直角三角形P F
 F
F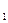 中,∠PF
中,∠PF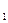 F
F =30
=30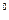
解法一:|F
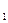 F
F |=
|=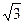 |P F
|P F |,即2c=
|,即2c=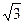
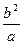 将c
将c =a
=a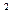 +b
+b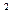 代入,解得b
代入,解得b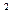 ="2" a
="2" a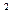
解法二:|PF
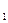 |="2|P" F
|="2|P" F |,由双曲线定义可知,|PF
|,由双曲线定义可知,|PF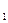 |-|P F
|-|P F |=2a,得|P F
|=2a,得|P F |=2a
|=2a∵|P F
 |=
|=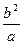 ,∴2a=
,∴2a=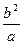 ,即b
,即b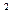 ="2" a
="2" a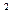 ∴
∴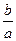 =
=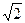
故所求双曲线的渐近线方程为y=±
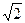 x 。
x 。
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
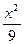 -
-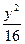 =1只有一个公共点的直线共有______________条.
=1只有一个公共点的直线共有______________条.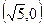 和曲线
和曲线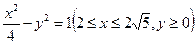 上的点
上的点 …、
…、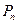 。若
。若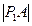 、
、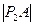 、…、
、…、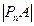 成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若
成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若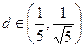 ,是否存在满足条件的
,是否存在满足条件的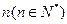 .若存在,求出n可取的所有值,若不存在,说明理由.
.若存在,求出n可取的所有值,若不存在,说明理由.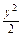 =1于A、B两点,且
=1于A、B两点,且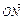 =
=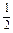 (
(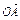 +
+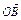 ).
).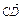 ·
·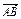 =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?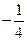
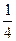
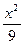 -
-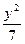 ="1(x>0)"
="1(x>0)"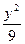 -
-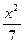 ="1(y>0)"
="1(y>0)"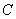 的方程为
的方程为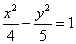 ,若直线
,若直线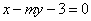 截双曲线的一支所得弦长为5
截双曲线的一支所得弦长为5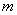 的值;
的值;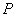 的直线与双曲线的两条渐近线分别交于
的直线与双曲线的两条渐近线分别交于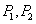 ,且点
,且点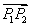 所成的比为
所成的比为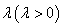 。当
。当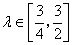 时,求
时,求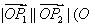 为坐标原点)的最大值和最小值
为坐标原点)的最大值和最小值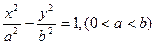 的半焦距为
的半焦距为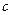 ,直线
,直线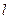 过点
过点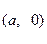 ,
,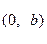 两点.已知原点到直线
两点.已知原点到直线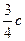 ,则双曲线的离心率为————
,则双曲线的离心率为————