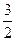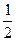题目内容
已知直线y=kx+1与双曲线x2-2y2=1有且仅有一个公共点,则实数k的值有( )
| A．1个 | B．2个 | C．3个 | D．4个 |
D
由
消去y得(1-2k2)x2-4kx-3=0.
若1-2k2≠0,则Δ=(4k)2-4(1-2k2)(-3)=0,得k=±
.
若1-2k2=0,得k=±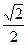
.
当k=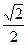时,得交点坐标为(-
,
);
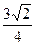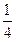当k=-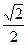时,得交点坐标为(,),
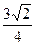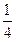即实数k共有4个值,故选择答案D.
消去y得(1-2k2)x2-4kx-3=0.若1-2k2≠0,则Δ=(4k)2-4(1-2k2)(-3)=0,得k=±
.若1-2k2=0,得k=±
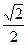.当k=
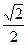时,得交点坐标为(-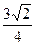,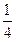);当k=-
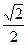时,得交点坐标为(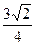,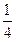),即实数k共有4个值,故选择答案D.
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
+
=1的焦点为顶点,顶点为焦点的双曲线方程是________________.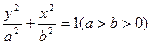
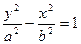上在第一象限内的一点，直线PA、PB分别交椭圆于C、D点，如果D恰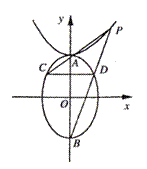
,并且与直线y=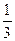
(x-4)相交所得线段的中点的横坐标为-
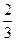,求这个双曲线的方程.
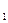、F
为双曲线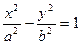
（a>0，b>0）的焦点，过F
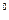，求双曲线的渐近线方程。
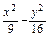=1有共同的渐近线，且过点（-3，2
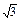）；求双曲线的标准方程.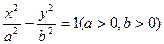
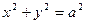
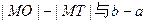
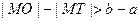
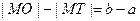
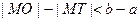
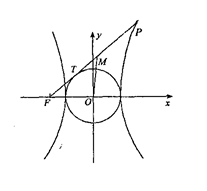
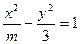的离心率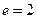
,则该双曲线两条准线间的距离为 ( )
