题目内容
(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD=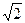 ,CD=1.
,CD=1.
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)证明:MC⊥BD;
(Ⅲ)求二面角A—PB—D的余弦值.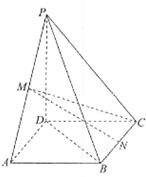
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD=
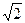 ,CD=1.
,CD=1.(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)证明:MC⊥BD;
(Ⅲ)求二面角A—PB—D的余弦值.

(1)略
(2)略
(3)
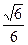
解:(Ⅰ)证明:取AD中点E,连接ME,NE,
由已知M,N分别是PA,BC的中点,
∴ME∥PD,NE∥CD
又ME,NE 平面MNE,ME
平面MNE,ME NE=E,
NE=E,
所以,平面MNE∥平面PCD,又MN 平面MNE
平面MNE
所以,MN∥平面PCD ……………4分
(Ⅱ)因为PD⊥平面ABCD,所以PD⊥DA,PD⊥DC,
在矩形ABCD中,AD⊥DC,
如图,以D为坐标原点,射线DA,DC,DP分别为
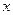 轴、
轴、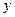 轴、
轴、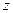 轴正半轴建立空间直角坐标系.
轴正半轴建立空间直角坐标系.
则D(0,0,0),A(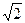 ,0,0),
,0,0),
B(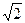 ,1,0),
,1,0),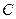 (0,1,0), P(0,0,
(0,1,0), P(0,0,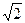 )
)
所以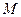 (
(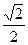 ,0,
,0,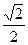 ),
),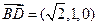 ,
,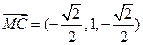
∵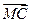 ·
· =0,所以MC⊥BD ……………8分
=0,所以MC⊥BD ……………8分
(Ⅲ)因为ME∥PD,所以ME⊥平面ABCD,ME⊥BD,又BD⊥MC,
所以BD⊥平面MCE, 所以CE⊥BD,又CE⊥PD,所以CE⊥平面PBD,
由已知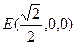 ,所以平面PBD的法向量
,所以平面PBD的法向量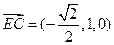
M为等腰直角三角形PAD斜边中点,所以DM⊥PA,
又CD⊥平面PAD,AB∥CD,所以AB⊥平面PAD,AB⊥DM,所以DM⊥平面PAB,
所以平面PAB的法向量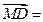 (-
(-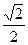 ,0,
,0, ),设二面角A—PB—D的平面角为θ,
),设二面角A—PB—D的平面角为θ,
则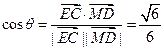 . 所以,二面角A—PB—D的余弦值为
. 所以,二面角A—PB—D的余弦值为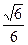 . ……………12分
. ……………12分
由已知M,N分别是PA,BC的中点,
∴ME∥PD,NE∥CD
又ME,NE
 平面MNE,ME
平面MNE,ME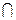 NE=E,
NE=E,所以,平面MNE∥平面PCD,又MN
 平面MNE
平面MNE所以,MN∥平面PCD ……………4分
(Ⅱ)因为PD⊥平面ABCD,所以PD⊥DA,PD⊥DC,
在矩形ABCD中,AD⊥DC,
如图,以D为坐标原点,射线DA,DC,DP分别为
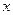 轴、
轴、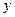 轴、
轴、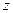 轴正半轴建立空间直角坐标系.
轴正半轴建立空间直角坐标系.则D(0,0,0),A(
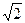 ,0,0),
,0,0),B(
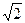 ,1,0),
,1,0),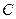 (0,1,0), P(0,0,
(0,1,0), P(0,0,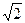 )
) 所以
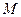 (
(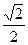 ,0,
,0,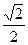 ),
),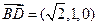 ,
,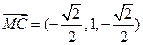
∵
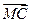 ·
· =0,所以MC⊥BD ……………8分
=0,所以MC⊥BD ……………8分(Ⅲ)因为ME∥PD,所以ME⊥平面ABCD,ME⊥BD,又BD⊥MC,
所以BD⊥平面MCE, 所以CE⊥BD,又CE⊥PD,所以CE⊥平面PBD,
由已知
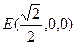 ,所以平面PBD的法向量
,所以平面PBD的法向量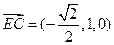
M为等腰直角三角形PAD斜边中点,所以DM⊥PA,
又CD⊥平面PAD,AB∥CD,所以AB⊥平面PAD,AB⊥DM,所以DM⊥平面PAB,
所以平面PAB的法向量
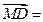 (-
(-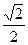 ,0,
,0, ),设二面角A—PB—D的平面角为θ,
),设二面角A—PB—D的平面角为θ,则
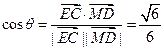 . 所以,二面角A—PB—D的余弦值为
. 所以,二面角A—PB—D的余弦值为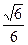 . ……………12分
. ……………12分
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
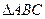 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边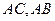 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.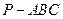 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥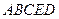 中,
中,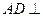 平面
平面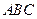 ,
,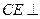 平面
平面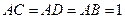 ,
,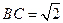 ,
,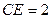 ,
,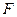 为
为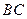 的中点.
的中点.
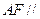 平面
平面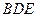 ;
;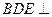 平面
平面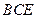 .
.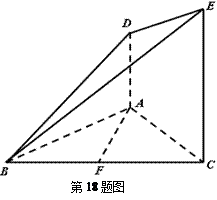
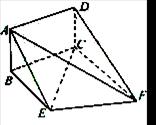
 BCF=
BCF=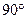 ,AD=
,AD=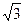 ,EF=2.
,EF=2. .
.
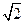 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 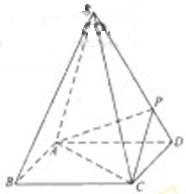
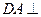 平面ABC,
平面ABC,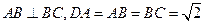 ,则球O的体积等于 。
,则球O的体积等于 。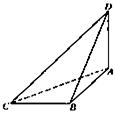
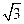 ,
,