题目内容
( 本题满分13分)
本题满分13分)
如图,点A、B分别是椭圆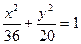 长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
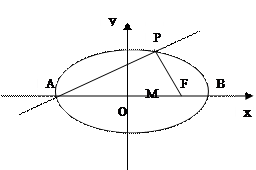
(1)求点P的坐标;
(2)设M椭圆长轴AB上的一点,M到直线AP的距离等于 ,求椭圆上的点到点M的距离d的最小值
,求椭圆上的点到点M的距离d的最小值
 本题满分13分)
本题满分13分)如图,点A、B分别是椭圆
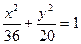 长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
(1)求点P的坐标;
(2)设M椭圆长轴AB上的一点,M到直线AP的距离等于
 ,求椭圆上的点到点M的距离d的最小值
,求椭圆上的点到点M的距离d的最小值(1)(
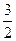 ,
, )
)(2)
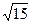
解(1)由已知可得点A(-6,0),F(0,4)
设点P(x,y),则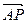 =(x+6,y),
=(x+6,y),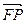 =(x-4,y),由已知可得
=(x-4,y),由已知可得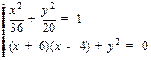
则2x2+9x-18=0,x=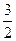 或x=-6. 由于y>0,只能x=
或x=-6. 由于y>0,只能x=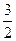 ,于是y=
,于是y= .
.
∴点P的坐标是(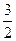 ,
, )
)
(2) 直线AP的方程是x-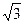 y+6="0. " 设点M(m,0),则M到直线AP的距离是
y+6="0. " 设点M(m,0),则M到直线AP的距离是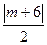 .
.
于是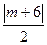 =
=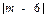 ,又-6≤m≤
,又-6≤m≤ 6,解得m=2.
6,解得m=2.
椭圆上的点(x,y)到点M的距离d有
d2=(x-2)2+y2=x-4x2+4+20- x2=
x2= (x-
(x- )2+15,
)2+15,
由于-6≤x≤6, ∴当x= 时,d取得最小值
时,d取得最小值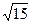 .
.
设点P(x,y),则
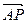 =(x+6,y),
=(x+6,y),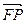 =(x-4,y),由已知可得
=(x-4,y),由已知可得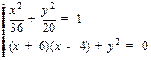
则2x2+9x-18=0,x=
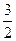 或x=-6. 由于y>0,只能x=
或x=-6. 由于y>0,只能x=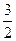 ,于是y=
,于是y= .
.∴点P的坐标是(
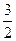 ,
, )
)(2) 直线AP的方程是x-
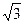 y+6="0. " 设点M(m,0),则M到直线AP的距离是
y+6="0. " 设点M(m,0),则M到直线AP的距离是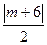 .
.于是
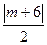 =
=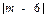 ,又-6≤m≤
,又-6≤m≤ 6,解得m=2.
6,解得m=2.椭圆上的点(x,y)到点M的距离d有
d2=(x-2)2+y2=x-4x2+4+20-
 x2=
x2= (x-
(x- )2+15,
)2+15,由于-6≤x≤6, ∴当x=
 时,d取得最小值
时,d取得最小值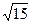 .
.
练习册系列答案
相关题目
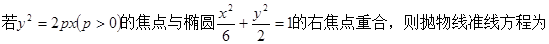 ( )
( )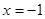
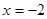
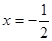
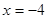
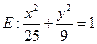 ,直线
,直线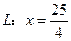 ,F为椭圆
,F为椭圆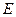 的右焦点,M为椭圆
的右焦点,M为椭圆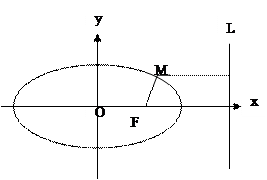
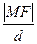 为定值;
为定值;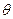 ,m交椭圆
,m交椭圆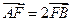 ,求
,求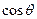 的值。
的值。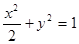 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则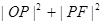 的最小值为_________
的最小值为_________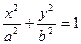 (a>b>0)
(a>b>0) ,一条准线方程为x=4 时,求椭圆方程;
,一条准线方程为x=4 时,求椭圆方程;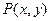 是椭圆上一点,在(1)的条件下,求
是椭圆上一点,在(1)的条件下,求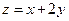 的最大值及相应的P点坐标。
的最大值及相应的P点坐标。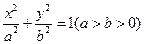 的左,右焦点为
的左,右焦点为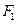 ,
,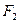 ,(1,
,(1,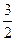 )为椭圆上一点,椭圆的
)为椭圆上一点,椭圆的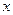 轴的对称点记为M,设
轴的对称点记为M,设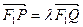 .
.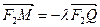 ;
;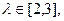 求|PQ|的取值范围
求|PQ|的取值范围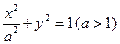 的两个焦点为F1,F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为
的两个焦点为F1,F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为 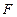 ,若椭圆上存在点
,若椭圆上存在点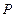 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段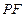 相切于线段
相切于线段

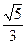
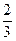
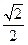
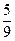
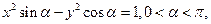 表示焦点在
表示焦点在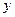 轴上的椭圆,则
轴上的椭圆,则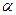 的取值范围是______ _____
的取值范围是______ _____