题目内容
7.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a-c)$\overrightarrow{BA}$•$\overrightarrow{BC}$=c$\overrightarrow{CB}$•$\overrightarrow{CA}$.(1)求角B的大小;
(2)若|$\overrightarrow{BA}$-$\overrightarrow{BC}$|=2$\sqrt{2}$,求|$\overrightarrow{BA}$|+|$\overrightarrow{BC}$|的最大值.
分析 (1)利用向量数量积的运算法则化简已知可得(2a-c)cosB=bcosC,然后利用正弦定理化简后,根据sinA不为0得到cosB的值,根据B的范围及特殊角的三角函数值即可求出B的度数;
(2)根据向量的减法法则,得到b2=8,然后根据余弦定理表示出b的平方,把b的平方代入后,利用基本不等式即可求出a+c的最大值.
解答 解:(1)∵(2a-c)$\overrightarrow{BA}$•$\overrightarrow{BC}$=c$\overrightarrow{CB}$•$\overrightarrow{CA}$,
∴(2a-c)cacosB=cabcosC,
∴(2a-c)cosB=bcosC,
根据正弦定理有(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB=sin(B+C)=sinA,
∵sinA>0,∴cosB=$\frac{1}{2}$,
∴B=$\frac{π}{3}$;
(2)∵|$\overrightarrow{BA}$-$\overrightarrow{BC}$|=2$\sqrt{2}$,∴b2=8,
根据余弦定理b2=a2+c2-2accosB,
可得8=a2+c2-ac,
∴(a+c)2-8=3ac
∵ac≤$(\frac{a+c}{2})^{2}$,
∴(a+c)2-8=$\frac{3}{4}$(a+c)2,
∴a+c≤4$\sqrt{2}$,
∴|$\overrightarrow{BA}$|+|$\overrightarrow{BC}$|的最大值为4$\sqrt{2}$.
点评 此题考查学生灵活运用平面向量的数量积的运算法则,灵活运用正弦、余弦定理及基本不等式是关键,是一道综合题.

练习册系列答案
相关题目
15.复数$z=\frac{i}{1-i}$在复平面上表示的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
12.复数${({\frac{1-i}{{\sqrt{2}}}})^{2015}}$计算的结果是( )
| A. | -1 | B. | -i | C. | $\frac{1+i}{{\sqrt{2}}}$ | D. | $\frac{-1+i}{{\sqrt{2}}}$ |
19.已知抛物线y2=8x的焦点与双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一个焦点重合,则该双曲线的离心率为( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{4\sqrt{15}}}{15}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{2}$ |
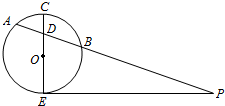 如图,CE为圆O的直径,PE为圆O的切线,E为切点,PBA为圆O的割线,交CE于D点,CD=2,AD=3,BD=4,则圆O的半径为r=4;PB=20.
如图,CE为圆O的直径,PE为圆O的切线,E为切点,PBA为圆O的割线,交CE于D点,CD=2,AD=3,BD=4,则圆O的半径为r=4;PB=20.