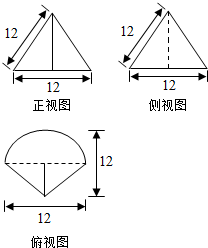
题目内容
2.已知抛物线y2=12x焦点的一条直线与抛物线相交于A、B两点,若|AB|=10,则线段AB的中点到y轴的距离等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设AB的中点为E,过 A、E、B 分别作准线的垂线,垂足分别为 C、G、D,如图所示,由EF为直角梯形的中位线及抛物线的定义求出EG,则 EH=EG-1 为所求.
解答  解:抛物线y2=12x焦点(3,0),准线为 l:x=-3,
解:抛物线y2=12x焦点(3,0),准线为 l:x=-3,
设AB的中点为E,过 A、E、B分别作准线的垂线,
垂足分别为 C、G、D,EF交纵轴于点H,如图所示:
则由EF为直角梯形的中位线知,
EG=$\frac{AC+BD}{2}$=$\frac{AF+BF}{2}$=$\frac{AB}{2}$=5,
∴EH=EG-3=5-3=2,
则AB的中点到y轴的距离等于2,
故选:B.
点评 本题考查直线与抛物线的位置关系,抛物线的简单性质的应用,体现了数形结合的数学思想,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
15.已知x,y∈R,则“x>y”是“|x|>|y|”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.已知{an}为等差数列,Sn为其前n项和.若a1=12,S6=S11,则必有( )
| A. | a17=0 | B. | a6+a12=0 | C. | S17>0 | D. | a9<0 |
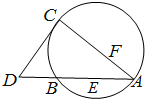 如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.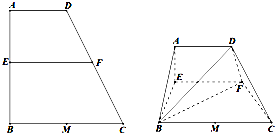 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.