题目内容
19.已知抛物线y2=8x的焦点与双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一个焦点重合,则该双曲线的离心率为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{4\sqrt{15}}}{15}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{2}$ |
分析 先求出抛物线y2=8x的焦点坐标F,从而得到双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一个焦点F,由此能求出a2,进而能求出此双曲线的离心率.
解答 解:抛物线y2=8x的焦点坐标为F(2,0),
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一个焦点与抛物线y2=8x的焦点重合,
∴双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一个焦点为F(2,0),
∴a2+1=4,解得a2=3,
∴此双曲线的离心率e=$\frac{2\sqrt{3}}{3}$.
故选:C.
点评 本题考查双曲线的离心率的求法,涉及到抛物线、双曲线的简单性质,是中档题.

练习册系列答案
相关题目
14.已知{an}为等差数列,Sn为其前n项和.若a1=12,S6=S11,则必有( )
| A. | a17=0 | B. | a6+a12=0 | C. | S17>0 | D. | a9<0 |
4.若复数z满足z(1+i)=1-i(i是虚数单位),则z的共轭复数$\overline{z}$的虚部是( )
| A. | -i | B. | -1 | C. | i | D. | 1 |
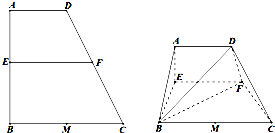 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.