题目内容
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数x都有
,且对任意的实数x都有![]() (e是自然对数的底数),且
(e是自然对数的底数),且![]() ,若关于x的不等式
,若关于x的不等式![]() 的解集中恰有两个整数,则实数m的取值范围是( )
的解集中恰有两个整数,则实数m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先利用导数等式结合条件![]() 求出函数
求出函数![]() 的解析式,由
的解析式,由![]() ,得
,得
![]() ,转化为函数
,转化为函数![]() 在直线
在直线![]() 下方的图象中只有两个横坐标为整数的点,然后利用导数分析函数
下方的图象中只有两个横坐标为整数的点,然后利用导数分析函数![]() 的单调性与极值,作出该函数的图象,利用数形结合思想求出实数
的单调性与极值,作出该函数的图象,利用数形结合思想求出实数![]() 的取值范围.
的取值范围.
由等式![]() ,可得
,可得![]() ,
,
即![]() ,即
,即![]() (
(![]() 为常数),
为常数),
![]() ,则
,则![]() ,
,![]() ,
,
因此,![]() ,
,![]() ,
,
令![]() ,得
,得![]() 或
或![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
| 极大值 |
|
函数![]() 的极小值为
的极小值为![]() ,极大值为
,极大值为![]() ,且
,且![]() ,
,
作出图象如下图所示,由图象可知,当![]() 时,
时,![]() .
.

另一方面![]() ,
,![]() ,则
,则![]() ,
,
由于函数![]() 在直线
在直线![]() 下方的图象中只有两个横坐标为整数的点,
下方的图象中只有两个横坐标为整数的点,
由图象可知,这两个点的横坐标分别为![]() 、
、![]() ,则有
,则有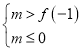 ,解得
,解得![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ,故选:B.
,故选:B.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目