题目内容
【题目】设![]()
(1)![]() 时,求过
时,求过![]() 的切线;
的切线;
(2)讨论函数![]() 的单调性;
的单调性;
(3)![]() 的零点个数少于
的零点个数少于![]() 个,求
个,求![]() 的取值范围.
的取值范围.
【答案】(1)切线方程为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)利用导数求出切线的斜率即得解;
(2)先求出导数![]() ,再对
,再对![]() 分类讨论即得解;
分类讨论即得解;
(3)先分离参数得到![]() ,再构造函数
,再构造函数![]() ,研究函数
,研究函数![]() 的单调性和图象即得解.
的单调性和图象即得解.
(1)![]() 时,
时,![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以切线方程为![]() .
.
所以切线方程为![]() .
.
(2)![]() .
.
所以![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() ,函数
,函数![]() 在R上单调递增;
在R上单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,
所以函数在![]() 上单调递增,在
上单调递增,在![]() 单调递减.
单调递减.
(3)![]() ,
,
因为![]() 时
时![]() ,即
,即![]() 不是函数的零点,
不是函数的零点,
所以![]() ,设
,设![]() ,
,
所以![]() ,
,
所以函数![]() 在
在![]() 单调递增,在
单调递增,在![]() ,
,![]() 单调递减,
单调递减,
当![]() 从左边趋近
从左边趋近![]() 时,
时,![]() ,当
,当![]() 从右边趋近
从右边趋近![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
又![]() ,画出
,画出![]() 的模拟图像如下所示:
的模拟图像如下所示:

所以当![]() 时,直线
时,直线![]() 和函数
和函数![]() 的图象的零点个数小于3个.
的图象的零点个数小于3个.
故![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】对于很多人来说,提前消费的认识首先是源于信用卡,在那个工资不高的年代,信用卡绝对是神器,稍微大件的东西都是可以选择用信用卡来买,甚至于分期买,然后慢慢还!现在银行贷款也是很风靡的,从房贷到车贷到一般的现金贷.信用卡“忽如一夜春风来”,遍布了各大小城市的大街小巷.为了解信用卡在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下![]() 列联表(单位:人)
列联表(单位:人)
经常使用信用卡 | 偶尔或不用信用卡 | 合计 | |
40岁及以下 | 15 | 35 | 50 |
40岁以上 | 20 | 30 | 50 |
合计 | 35 | 65 | 100 |
(1)根据以上数据,能否在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关?
市使用信用卡情况与年龄有关?
(2)①现从所抽取的40岁及以下的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出4人赠送积分,求选出的4人中至少有3人偶尔或不用信用卡的概率;
②将频率视为概率,从![]() 市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为
市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
参考公式: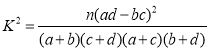 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某蛋糕店计划按天生产一种面包,每天生产量相同,生产成本每个6元,售价每个8元,未售出的面包降价处理,以每个5元的价格当天全部处理完.
(1)若该蛋糕店一天生产30个这种面包,求当天的利润y(单位:元)关于当天需求量n(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)蛋糕店记录了30天这种面包的日需求量(单位:个),整理得表:
日需求量n | 28 | 29 | 30 | 31 | 32 | 33 |
频数 | 3 | 4 | 6 | 6 | 7 | 4 |
假设蛋糕店在这30天内每天生产30个这种面包,求这30天的日利润(单位:元)的平均数及方差;
(3)蛋糕店规定:若连续10天的日需求量都不超过10个,则立即停止这种面包的生产,现给出连续10天日需求量的统计数据为“平均数为6,方差为2”,试根据该统计数据决策是否一定要停止这种面包的生产?并给出理由.
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
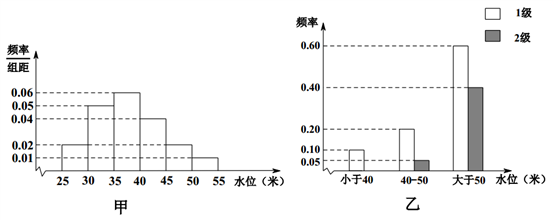
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.