题目内容
10.已知函数f(x)=($\frac{1}{2}$)|x-1|+a|x+2|.当a=1时,f(x)的单调递减区间为[1,+∞);当a=-1时,f(x)的单调递增区间为[-2,1],f(x)的值域为[$\frac{1}{8}$,8].分析 当a=1时,f(x)=($\frac{1}{2}$)|x-1|+|x+2|,令u(x)=|x-1|+|x+2|=$\left\{\begin{array}{l}{2x+1,x≥1}\\{3,-2≤x≤1}\\{-2x-1,x<-2}\end{array}\right.$,利用复合函数的单调性判断即可;当a=-1时,f(x)=($\frac{1}{2}$)|x-1|-|x+2|令u(x)=|x-1|-|x+2|=$\left\{\begin{array}{l}{-3,x≥1}\\{-2x-1,-2≤x<2}\\{3,x≤-2}\end{array}\right.$,根据复合函数的单调性可判断即可.
解答 解:(1)∵f(x)=($\frac{1}{2}$)|x-1|+a|x+2|.
∴当a=1时,f(x)=($\frac{1}{2}$)|x-1|+|x+2|,
令u(x)=|x-1|+|x+2|=$\left\{\begin{array}{l}{2x+1,x≥1}\\{3,-2≤x≤1}\\{-2x-1,x<-2}\end{array}\right.$,
∴u(x)在[1,+∞)单调递增,
根据复合函数的单调性可判断:f(x)的单调递减区间为[1,+∞),
(2)当a=-1时,f(x)=($\frac{1}{2}$)|x-1|-|x+2|
令u(x)=|x-1|-|x+2|=$\left\{\begin{array}{l}{-3,x≥1}\\{-2x-1,-2≤x<2}\\{3,x≤-2}\end{array}\right.$,
u(x)在[-2,1]单调递减,
∴根据复合函数的单调性可判断:f(x)的单调递增区间为[-2,1],f(x)的值域为[$\frac{1}{8}$,8].
故答案为:[1,+∞);[-2,1];[$\frac{1}{8}$,8].
点评 本题考查了函数的单调性,复合函数的单调性的判断,属于中档题,关键是去绝对值.

 口算能手系列答案
口算能手系列答案| A. | (-3,+∞) | B. | $(-∞,\frac{1}{2})$ | C. | (-3,1) | D. | (0,1) |
| A. | [$\frac{\sqrt{2}-2}{2}$,3] | B. | [$\frac{\sqrt{2}}{2}$,4] | C. | [-$\frac{1}{2}$,15] | D. | [$\frac{1}{2}$,16] |
| A. | 0=∅ | B. | ∅={0} | C. | 0∈∅ | D. | ∅⊆{0} |
| A. | 3 | B. | $\frac{5}{2}$ | C. | -3 | D. | $-\frac{5}{2}$ |
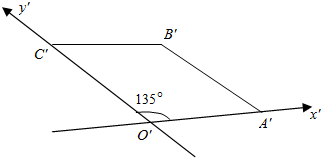 在直观图如图中,四边形O′A′B′C′为菱形且边长为2cm,则在xOy坐标系中原四边形OABC为矩形(填形状),面积为8cm2.
在直观图如图中,四边形O′A′B′C′为菱形且边长为2cm,则在xOy坐标系中原四边形OABC为矩形(填形状),面积为8cm2.