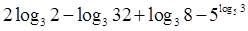题目内容
(本小题满分12分)
已知函数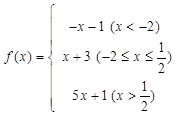 (
(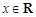 ),
),
(Ⅰ)求函数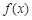 的最小值;
的最小值;
(Ⅱ)已知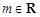 ,
,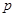 :关于
:关于 的不等式
的不等式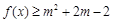 对任意
对任意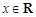 恒成立;
恒成立;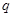 :函数
:函数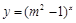 是增函数.若“
是增函数.若“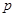 或
或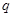 ”为真,“
”为真,“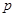 且
且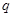 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
(Ⅰ)1;(Ⅱ)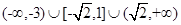 。
。
解析试题分析:(Ⅰ)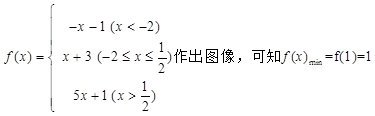 (4分)
(4分)
(Ⅱ)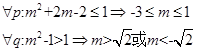 (8分)
(8分)
由于 (10分)
(10分)
故实数 的取值范围是
的取值范围是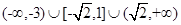 (12分)
(12分)
考点:分段函数最值的求法;恒成立的问题;复合命题真假的判断。
点评:(1)分段函数的最值,要分段求,最后在进行比较;(2)解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: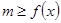 在
在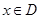 上恒成立
上恒成立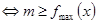 ;思路2:
;思路2: 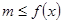 在
在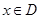 上恒成立
上恒成立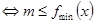 。
。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 ,
,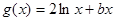 ,且直线
,且直线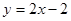 与曲线
与曲线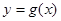 相切.
相切. 内的一切实数
内的一切实数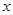 ,不等式
,不等式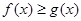 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;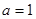 时,求最大的正整数
时,求最大的正整数 ,使得对
,使得对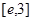 (
(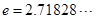 是自然对数的底数)内的任意
是自然对数的底数)内的任意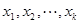 都有
都有 成立;
成立;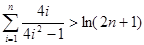
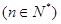 .
. ;
;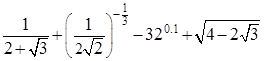 .
.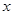 小时的收费为
小时的收费为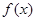 元
元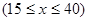 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动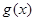 元
元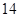 分)已知函数
分)已知函数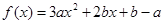 (
( ,
,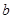 是不同时为零的常数).
是不同时为零的常数).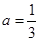 时,若不等式
时,若不等式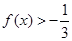 对任意
对任意 恒成立,求实数
恒成立,求实数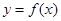 在
在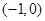 内至少存在一个零点.
内至少存在一个零点.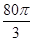 立方米,且
立方米,且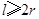 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为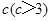 千元,设该容器的建造费用为
千元,设该容器的建造费用为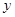 千元.
千元.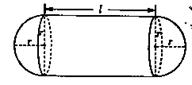
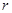 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;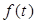 (元)与时间
(元)与时间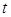 (天)的函数关系近似满足
(天)的函数关系近似满足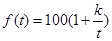 (
(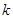 为正的常数),日销售量
为正的常数),日销售量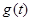 (件)与时间
(件)与时间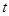 (天)的函数关系近似满足
(天)的函数关系近似满足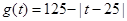 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.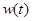 关于时间
关于时间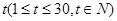 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额 ,
, 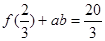 ,且
,且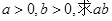 的取值范围
的取值范围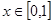 时,
时, 恒成立,且
恒成立,且 的取值范围
的取值范围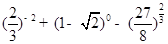 ;
;