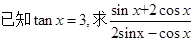题目内容
(本小题满分13分)经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格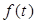 (元)与时间
(元)与时间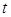 (天)的函数关系近似满足
(天)的函数关系近似满足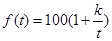 (
(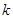 为正的常数),日销售量
为正的常数),日销售量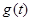 (件)与时间
(件)与时间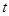 (天)的函数关系近似满足
(天)的函数关系近似满足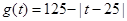 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.
(1)求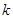 的值;
的值;
(2)试写出该商品的日销售金额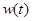 关于时间
关于时间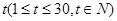 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额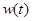 的最小值。
的最小值。
(1)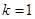 ;(2
;(2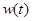 =
=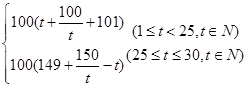 ,
,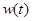 有最小值12100 元。
有最小值12100 元。
解析试题分析:(1)由题意,得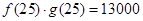 ,即
,即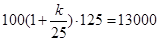 ,
,
解得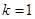 ……4分
……4分
(2)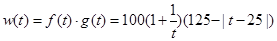
=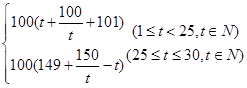 ……9分
……9分
当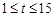 时,
时,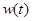 在
在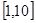 上单调减,在
上单调减,在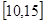 上单调增
上单调增
所以当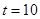 时,
时,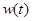 有最小值12100 元……………13分
有最小值12100 元……………13分
考点:函数的实际应用;分段函数。函数的单调性及最值。
点评:研究数学模型,建立数学模型,进而借鉴数学模型,对提高解决实际问题的能力,以及提高数学素养都是十分重要的.建立模型的步骤可分为: (1) 分析问题中哪些是变量,哪些是常量,分别用字母表示; (2) 根据所给条件,运用数学知识,确定等量关系; (3) 写出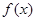 的解析式并指明定义域。
的解析式并指明定义域。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
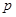 (万元)和
(万元)和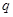 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: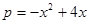 ,
, 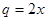 今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元? =
=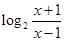 .
.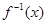 ,并求使得函数
,并求使得函数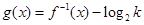 有零点的实数
有零点的实数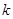 的取值范围.
的取值范围.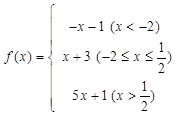 (
(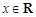 ),
),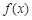 的最小值;
的最小值;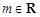 ,
,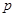 :关于
:关于 的不等式
的不等式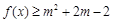 对任意
对任意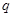 :函数
:函数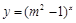 是增函数.若“
是增函数.若“ 的取值范围.
的取值范围.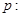 方程
方程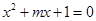 有两个不等的正实数根,命题
有两个不等的正实数根,命题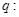 方程
方程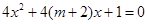 无实数根。若“
无实数根。若“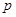 或
或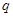 ”为真命题,求
”为真命题,求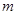 的取值范围。
的取值范围。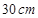 的
的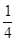 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料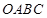 ,其中点
,其中点 在圆上,点
在圆上,点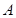 、
、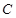 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长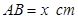 ,圆柱的体积为
,圆柱的体积为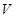
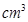 .
.
 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;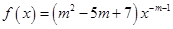
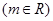 为偶函数.
为偶函数.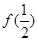 的值;
的值;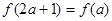 ,求实数
,求实数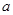 的值.
的值.