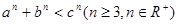题目内容
(本小题满分16分)
已知 ,
,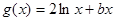 ,且直线
,且直线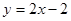 与曲线
与曲线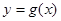 相切.
相切.
(1)若对 内的一切实数
内的一切实数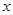 ,不等式
,不等式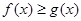 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当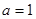 时,求最大的正整数
时,求最大的正整数 ,使得对
,使得对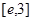 (
(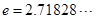 是自然对数的底数)内的任意
是自然对数的底数)内的任意 个实数
个实数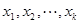 都有
都有 成立;
成立;
(3)求证: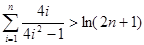
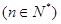 .
.
(1)设点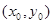 为直线
为直线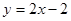 与曲线
与曲线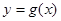 的切点,则有
的切点,则有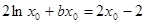 . (*)
. (*)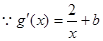 ,
,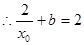 . (**)
. (**)
由(*)、(**)两式,解得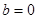 ,
,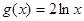 .
.
由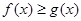 整理,得
整理,得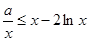 ,
,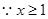 ,
,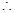 要使不等式
要使不等式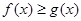 恒成立,必须
恒成立,必须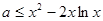 恒成立.
恒成立.
设 ,
,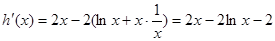 ,
,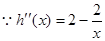 ,
,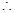 当
当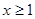 时,
时,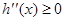 ,则
,则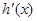 是增函数,
是增函数,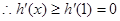 ,
,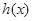 是增函数,
是增函数, ,
,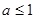 .
.
因此,实数 的取值范围是
的取值范围是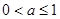 .
.
(2)当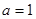 时,
时,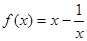
 ,
,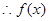 在
在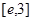 上是增函数,
上是增函数,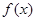 在
在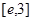 上的最大值为
上的最大值为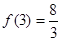 .
.
要对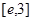 内的任意
内的任意 个实数
个实数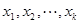 都有
都有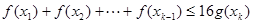
成立,必须使得不等式左边的最大值小于或等于右边的最小值,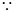 当
当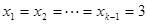 时不等式左边取得最大值,
时不等式左边取得最大值,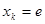 时不等式右边取得最小值.
时不等式右边取得最小值. ,解得
,解得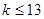 .因此,
.因此, 的最大值为
的最大值为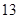 .
.
(3)证明:当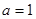 时,得出
时,得出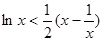 . 令
. 令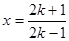 ,
,
化简得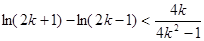 ,
,
得出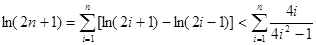 .
.
解析试题分析:(1)设点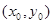 为直线
为直线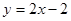 与曲线
与曲线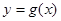 的切点,则有
的切点,则有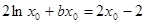 . (*)
. (*)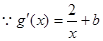 ,
,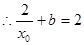 . (**)
. (**)
由(*)、(**)两式,解得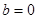 ,
,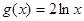 .
.
由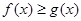 整理,得
整理,得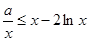 ,
,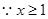 ,
,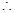 要使不等式
要使不等式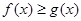 恒成立,必须
恒成立,必须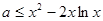 恒成立.
恒成立.
设 ,
,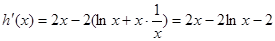 ,
,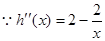 ,
,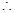 当
当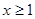 时,
时,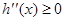 ,则
,则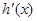 是增函数,
是增函数,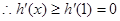 ,
,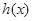 是增函数,
是增函数, ,
,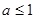 .
.
因此,实数 的取值范围是
的取值范围是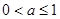 .
.
(2)当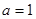 时,
时,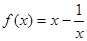
 ,
,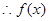 在
在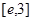 上是增函数,
上是增函数,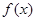 在
在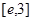 上的最大值为
上的最大值为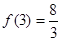 .
.
要对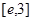 内的任意
内的任意 个实数
个实数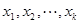 都有
都有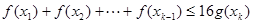
成立,必须使得不等式左边的最大值小于或等于右边的最小值,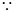 当
当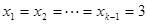 时不等式左边取得最大值,
时不等式左边取得最大值,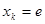 时不等式右边取得最小值.
时不等式右边取得最小值. ,解得
,解得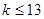 .因此,
.因此, 的最大值为
的最大值为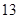 .
.
(3)证明:当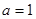 时,根据(1)的推导有,
时,根据(1)的推导有,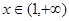 时,
时, ,
,
即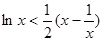 . 令
. 令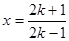 ,得
,得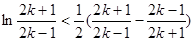 ,
,
化简得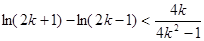 ,
, 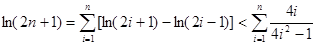 .
.
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性及极值,证明不等式。
点评:典型题,本题属于导数应用中的基本问题,像涉及恒成立问题,往往通过研究函数的最值达到解题目的。证明不等式问题,往往通过构造新函数,研究其单调性及最值,而达到目的。本题涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目

 个月的旅游人数的和
个月的旅游人数的和 (单位:万人)与
(单位:万人)与 已知第
已知第 (单位:元)与
(单位:元)与
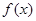 (单位:万人)与x的函数关系式;
(单位:万人)与x的函数关系式;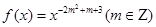 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数. 的值,并确定
的值,并确定 的解析式;
的解析式; 且
且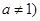 ,是否存在实数
,是否存在实数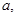 使
使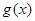 在区间
在区间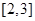 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: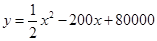 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.  (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点. ·
·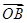 的值;
的值; 、
、 的终边上,求tan(
的终边上,求tan(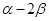 )的值.
)的值.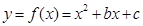 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线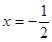 对称。
对称。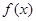 的解析式。
的解析式。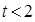 ,
,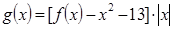 ,
,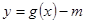 的零点有三个,求实数
的零点有三个,求实数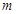 的取值范围;
的取值范围;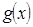 在[
在[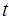 ,2]上的最小值。
,2]上的最小值。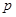 (万元)和
(万元)和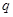 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: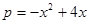 ,
, 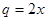 今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元? (
( ),
),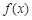 的最小值;
的最小值; ,
,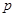 :关于
:关于 的不等式
的不等式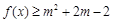 对任意
对任意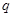 :函数
:函数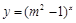 是增函数.若“
是增函数.若“ 的取值范围.
的取值范围.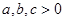 , 且
, 且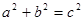 ,求证:
,求证: