题目内容
已知数列 满足:当
满足:当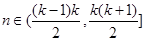 (
(
 )时,
)时, ,
, 是数列
是数列 的前
的前 项和,定义集合
项和,定义集合 是
是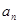 的整数倍,
的整数倍, ,且
,且
 ,
, 表示集合
表示集合 中元素的个数,则
中元素的个数,则 ,
, .
.
9, 1022
解析试题分析:由于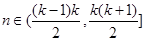 (
(
 )时,
)时, ,可知数列
,可知数列 满足:
满足: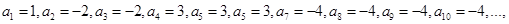 ,其前n项和
,其前n项和 满足:
满足:
当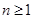 时,
时,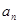 是奇数,则
是奇数,则 是
是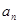 的整数倍;
的整数倍;
所以当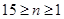 时,
时,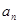 的奇数项共有9项,故
的奇数项共有9项,故 9;所以当
9;所以当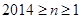 时,
时,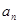 的奇数项共有1022项,故
的奇数项共有1022项,故 1022;
1022;
考点:1.集合的表示法;2.数列通项与前n项和的关系;3.数学归纳法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的各项均为正整数,对于
的各项均为正整数,对于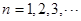 ,有
,有 ,
,  ,当
,当 且
且 为奇数时,
为奇数时, ,则
,则 令
令 令当n>1时,
令当n>1时, 则
则 ,
,  .
.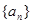 的前
的前 项和
项和 (
( ),则
),则 的值是__________.
的值是__________. 中,
中, ,且
,且 ,则
,则 的值为 .
的值为 .  的首项
的首项 ,前n项和为Sn ,且满足
,前n项和为Sn ,且满足 ( n∈N*) .则满足
( n∈N*) .则满足 的所有n的和为 .
的所有n的和为 .