题目内容
已知数列 中,
中, ,且
,且 ,则
,则 的值为 .
的值为 .
1
解析试题分析: 由
由 ,得
,得 ,由
,由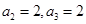
得 ,由
,由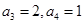 得
得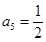 ,由
,由 得
得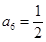 ,由
,由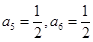
得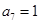 ,
, 得
得 由此推理可得
由此推理可得 是一个周期为
是一个周期为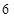 的数列,所以
的数列,所以
考点:数列的递推公式和求值.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
题目内容
已知数列 中,
中, ,且
,且 ,则
,则 的值为 .
的值为 .
1
解析试题分析: 由
由 ,得
,得 ,由
,由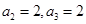
得 ,由
,由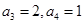 得
得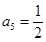 ,由
,由 得
得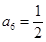 ,由
,由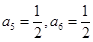
得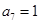 ,
, 得
得 由此推理可得
由此推理可得 是一个周期为
是一个周期为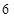 的数列,所以
的数列,所以
考点:数列的递推公式和求值.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案