题目内容
设数列 的首项
的首项 ,前n项和为Sn ,且满足
,前n项和为Sn ,且满足 ( n∈N*) .则满足
( n∈N*) .则满足 的所有n的和为 .
的所有n的和为 .
7
解析试题分析:由题意 ,可得:
,可得: 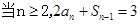 ,与原式相减得:
,与原式相减得: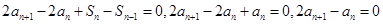 ,故
,故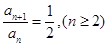 ,又
,又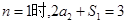 ,得
,得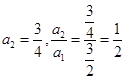 ,所以
,所以 是等比数列,可得
是等比数列,可得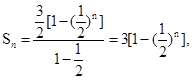 有
有 ,则
,则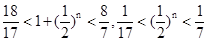 ,解得
,解得 ,所以和为
,所以和为
考点:1.等比数列的运算;2.指数不等式

练习册系列答案
相关题目
题目内容
设数列 的首项
的首项 ,前n项和为Sn ,且满足
,前n项和为Sn ,且满足 ( n∈N*) .则满足
( n∈N*) .则满足 的所有n的和为 .
的所有n的和为 .
7
解析试题分析:由题意 ,可得:
,可得: 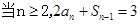 ,与原式相减得:
,与原式相减得: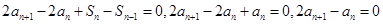 ,故
,故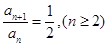 ,又
,又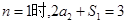 ,得
,得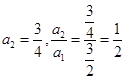 ,所以
,所以 是等比数列,可得
是等比数列,可得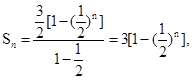 有
有 ,则
,则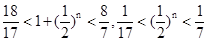 ,解得
,解得 ,所以和为
,所以和为
考点:1.等比数列的运算;2.指数不等式
