题目内容
已知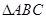 的三个顶点均在球O的球面上,且AB=AC=1,
的三个顶点均在球O的球面上,且AB=AC=1,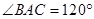 ,直线OA与平面ABC所成的角的正弦值为
,直线OA与平面ABC所成的角的正弦值为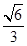 ,则球面上B、C两点间的球面距离为 。
,则球面上B、C两点间的球面距离为 。
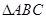 的三个顶点均在球O的球面上,且AB=AC=1,
的三个顶点均在球O的球面上,且AB=AC=1,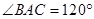 ,直线OA与平面ABC所成的角的正弦值为
,直线OA与平面ABC所成的角的正弦值为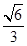 ,则球面上B、C两点间的球面距离为 。
,则球面上B、C两点间的球面距离为 。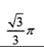
分析:欲求球面上B、C两点间的球面距离,作出O到平面ABC的高,判断垂足O′是外心,然后解三角形ABC的外接圆半径和球心角,最后求得P到球面上B、C两点间的球面距离.
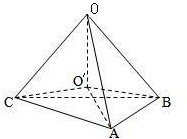
解:在三角形ABC中,AB=AC=1,∠BAC=120°,
∴由余弦定理得BC=
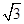 ,
,由正弦定理得,三角形ABC外接圆的半径O′B=
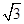 ,如图,
,如图,又直线OA与平面ABC所成的角的正弦值为
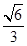 ,
,∴
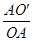 =cos∠OAO′,解得OA=
=cos∠OAO′,解得OA=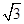 ,
,在三角形BCO′中,
∠BO′C=
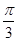 ,球的半径R=
,球的半径R=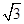 ,
,则球面上B、C两点间的球面距离为:
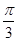 ×
×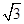 =
= π
π故答案为:
 π.
π.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
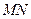 和
和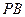 是两条面对角线,请在图(2)的正方体中将
是两条面对角线,请在图(2)的正方体中将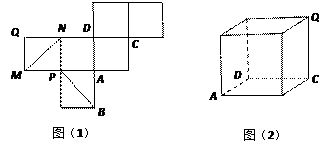
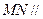 平面
平面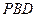 ;
;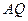 ⊥平面
⊥平面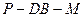 的大小.
的大小.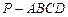 的底面
的底面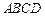 为菱形,
为菱形,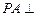 平面
平面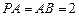 ,
,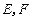 分别为
分别为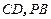 的中点,
的中点,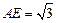 .
.
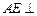 平面
平面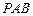 .
.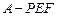 的体积.
的体积.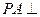 平面ABC,
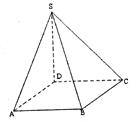
平面ABC, 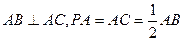 ,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。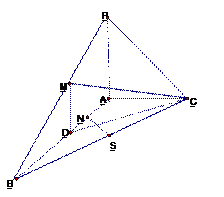
 平面CDM.
平面CDM.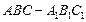 中,已知
中,已知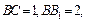
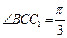 ,
,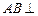 侧面
侧面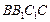 。
。
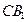 与底面ABC所成角正切值;
与底面ABC所成角正切值;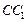 (不包含端点
(不包含端点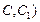 上确定一点
上确定一点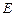 的位置,使得
的位置,使得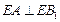 (要求说明理由).
(要求说明理由). 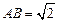 ,求二面角
,求二面角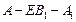 的大小.
的大小.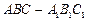 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是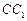 的中点,直线
的中点,直线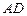 与侧面
与侧面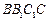 所成的角是
所成的角是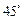 .
.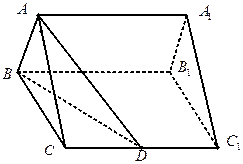
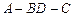 的大小;
的大小;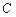 到平面
到平面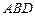 的距离.
的距离. 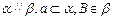 ,则在
,则在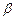 内过点B的所有直线中( )
内过点B的所有直线中( )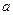 平行的直线
平行的直线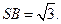
 (本小题满分12分)
(本小题满分12分) 平面ABCD,PD=AD=2。
平面ABCD,PD=AD=2。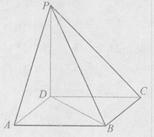
 平面ADE?并说明理由。
平面ADE?并说明理由。