题目内容
已知三棱锥P-ABC中,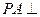 平面ABC,
平面ABC, 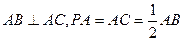 ,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
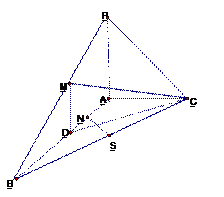
(1)求证: PA//平面CDM;
(2)求证: SN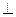 平面CDM.
平面CDM.
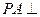 平面ABC,
平面ABC, 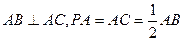 ,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
,N为AB上一点,AB=" 4AN," M ,D ,S分别为PB,AB,BC的中点。
(1)求证: PA//平面CDM;
(2)求证: SN
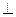 平面CDM.
平面CDM.(1)证明:在三棱锥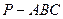 中
中
因为M,D,分别为PB,AB的中点,
所以
因为
所以 ……………………………………….5分
……………………………………….5分
(2)证明:因为M,D,分别为PB,AB的中点
所以
因为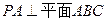
所以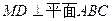
又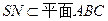
所以 ……………………………………………………9分
……………………………………………………9分
在△ABC中,连接DS
因为D,S分别为AB,BC的中点
所以,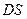 ∥AC且
∥AC且




又AB⊥AC,所以, .
.
因为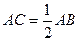
所以AC=AD
所以,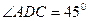 ,因此
,因此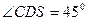 .
.
又AB=4AN
所以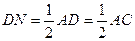
即DN=DS,故 ……………………………………………………12分
……………………………………………………12分
又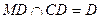




 所以
所以
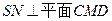 ………… ………………………. ……………………….13分
………… ………………………. ……………………….13分
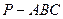 中
中因为M,D,分别为PB,AB的中点,
所以

因为

所以
 ……………………………………….5分
……………………………………….5分(2)证明:因为M,D,分别为PB,AB的中点
所以

因为
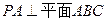
所以
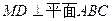
又
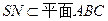
所以
 ……………………………………………………9分
……………………………………………………9分在△ABC中,连接DS
因为D,S分别为AB,BC的中点
所以,
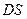 ∥AC且
∥AC且




又AB⊥AC,所以,
 .
.
因为
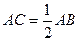
所以AC=AD
所以,
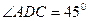 ,因此
,因此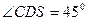 .
.又AB=4AN
所以
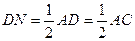
即DN=DS,故
 ……………………………………………………12分
……………………………………………………12分又
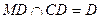




 所以
所以
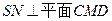 ………… ………………………. ……………………….13分
………… ………………………. ……………………….13分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
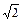 ,AB⊥AC
,AB⊥AC 求异面直线BC1与AC所成角的度数
求异面直线BC1与AC所成角的度数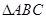 的三个顶点均在球O的球面上,且AB=AC=1,
的三个顶点均在球O的球面上,且AB=AC=1,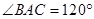 ,直线OA与平面ABC所成的角的正弦值为
,直线OA与平面ABC所成的角的正弦值为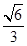 ,则球面上B、C两点间的球面距离为 。
,则球面上B、C两点间的球面距离为 。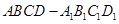 中,底面为正方形,侧棱垂直于底面,
中,底面为正方形,侧棱垂直于底面,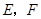 分别是
分别是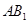 ,
,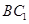 的中点,则以下结论中不成立的为( ).
的中点,则以下结论中不成立的为( ).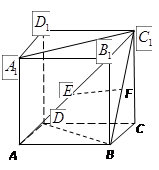
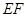 与
与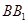 垂直
垂直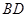 垂直
垂直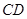 异面
异面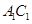 异面
异面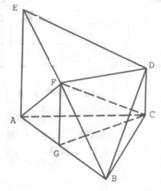
 BD=
BD=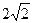 .
.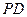 上是否存在一点
上是否存在一点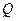 ,使
,使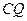 与平面
与平面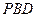 所成的角的正弦值为
所成的角的正弦值为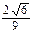 ,若存在,指出点
,若存在,指出点
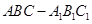 中,底面边长和侧棱都是2,D是侧棱
中,底面边长和侧棱都是2,D是侧棱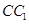 上任意一点.E是
上任意一点.E是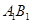 的中点.
的中点.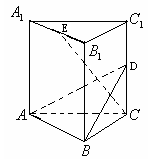
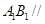 (1)求证: 平面ABD;
(1)求证: 平面ABD;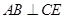 (2)求证: ;
(2)求证: ;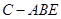 的体积。
的体积。