题目内容
12.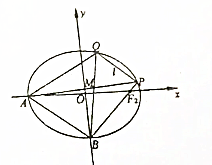 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,右焦点、下顶点、左顶点分别为F2,B,A,AB=$\sqrt{3}$,直线l交椭圆C与P,Q两点,直线AP与BQ交于点M.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,右焦点、下顶点、左顶点分别为F2,B,A,AB=$\sqrt{3}$,直线l交椭圆C与P,Q两点,直线AP与BQ交于点M.(1)求a,b的值;
(2)当BP过点F2时,求过A,B,P三点的圆的方程;
(3)当$\frac{AM}{MP}$=$\frac{BM}{MQ}$时,求F2M的最小值.
分析 (1)运用椭圆的离心率公式和a,b,c的关系,解方程可得a,b;
(2)求出椭圆方程,将直线y=x-1代入椭圆方程,求得P的坐标,设圆的一般式方程,运用待定系数法,解得参数d,e,f即可得到所求圆的方程;
(3)由三角形相似可得AB∥PQ,求得PQ的斜率,设出P,Q的方程,运用点差法,同时运用向量共线的坐标表示,求得点M的轨迹方程,再由点到直线的距离公式,即可得到所求的最小值.
解答 解:(1)由椭圆方程可得A(-a,0),B(0,-b),
由题意可得a2+b2=3,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,
解得a=$\sqrt{2}$,b=1;
(2)椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,
即有B(0,-1),F2(1,0),
直线BF2:y=x-1,
代入椭圆方程可得,3x2-4x=0,
解得x=$\frac{4}{3}$,y=$\frac{1}{3}$.
即有P($\frac{4}{3}$,$\frac{1}{3}$),A(-$\sqrt{2}$,0),
设过A,B,P三点的圆的方程为x2+y2+dx+ey+f=0,
则$\left\{\begin{array}{l}{2-\sqrt{2}d+f=0}\\{1-e+f=0}\\{\frac{17}{9}+\frac{4}{3}d+\frac{1}{3}e+f=0}\end{array}\right.$解得$\left\{\begin{array}{l}{d=\frac{\sqrt{2}-1}{3}}\\{e=-\frac{1+\sqrt{2}}{3}}\\{f=-\frac{4+\sqrt{2}}{3}}\end{array}\right.$,
即有所求圆的方程为x2+y2+$\frac{\sqrt{2}-1}{3}$x-$\frac{\sqrt{2}+1}{3}$y-$\frac{4+\sqrt{2}}{3}$=0;
(3)由$\frac{AM}{MP}$=$\frac{BM}{MQ}$,∠AMB=∠PMQ,
即有△AMB∽△PMQ,则∠MAB=∠MPQ,
即有PQ∥AB,
即有kPQ=kAB=-$\frac{\sqrt{2}}{2}$,
设P(x1,y1),Q(x2,y2),
则x12+2y12=2,x22+2y22=2,
两式相减可得,(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0,
$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=-$\frac{2({y}_{1}-{y}_{2})}{{x}_{1}-{x}_{2}}$=-2×(-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$,
又设$\frac{AM}{MP}$=$\frac{BM}{MQ}$=t,t>0,M(x,y),
则$\overrightarrow{AM}$=t$\overrightarrow{MP}$,$\overrightarrow{BM}$=t$\overrightarrow{MQ}$,
由A(-$\sqrt{2}$,0),B(0,-1),M(x,y),P(x1,y1),Q(x2,y2),
即有x+$\sqrt{2}$=t(x1-x),x=t(x2-x),
相加可得2x+$\sqrt{2}$=t(x1+x2),①
由y=t(y1-y),y+1=t(y2-y),
相加可得2y+1=t(y1+y2),②
①÷②可得,$\frac{2x+\sqrt{2}}{2y+1}$=$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=$\sqrt{2}$,
即有x-$\sqrt{2}$y=0,
即为点M的轨迹方程.
又F2(1,0),F2到直线x-$\sqrt{2}$y=的距离为d=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
即有F2M的最小值为$\frac{\sqrt{3}}{3}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,注意运用点差法,以及向量的共线坐标表示,同时考查直线和圆方程的求法,考查运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
| A. | 8 | B. | 15 | C. | 16 | D. | 32 |
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |