题目内容
17.若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为( )| A. | 8 | B. | 15 | C. | 16 | D. | 32 |
分析 根据标准差和方差之间的关系先求出对应的方差,然后结合变量之间的方差关系进行求解即可.
解答 解:∵样本数据x1,x2,…,x10的标准差为8,
∴$\sqrt{DX}$=8,即DX=64,
数据2x1-1,2x2-1,…,2x10-1的方差为D(2X-1)=4DX=4×64,
则对应的标准差为$\sqrt{D(2X-1)}$=$\sqrt{4×64}$=16,
故选:C.
点评 本题主要考查方差和标准差的计算,根据条件先求出对应的方差是解决本题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
5.若复数$\frac{1+bi}{2+i}$是纯虚数(i是虚数单位,b是实数),则b=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
9.设函数f(x)=$\left\{\begin{array}{l}{3x-b,x<1}\\{{2}^{x},x≥1}\end{array}\right.$,若f(f($\frac{5}{6}$))=4,则b=( )
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
6.设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A∪B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x<1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
7.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况
注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每100千米平均耗油量为 ( )
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2015年5月1日 | 12 | 35000 |
| 2015年5月15日 | 48 | 35600 |
| A. | 6升 | B. | 8升 | C. | 10升 | D. | 12升 |
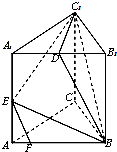 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,右焦点、下顶点、左顶点分别为F2,B,A,AB=$\sqrt{3}$,直线l交椭圆C与P,Q两点,直线AP与BQ交于点M.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,右焦点、下顶点、左顶点分别为F2,B,A,AB=$\sqrt{3}$,直线l交椭圆C与P,Q两点,直线AP与BQ交于点M.