题目内容
2.已知函数$f(x)={x^2}+\frac{a}{x}$(a∈R).(1)判断f(x)的奇偶性;
(2)当a=1时,求证:函数y=f(x)在区间$({0,\root{3}{{\frac{1}{2}}}})$上是单调递减函数,在区间($\root{3}{\frac{1}{2}}$,+∞)上是单调递增函数;
(3)若正实数x,y,z满足x+y2=z,x2+y=z2,求z的最小值.
分析 (1)根据函数奇偶性的定义进行判断即可.
(2)根据函数单调性的定义进行证明即可.
(3)利用消元法结合函数单调性的性质进行求解.
解答 解:(1)由$f(x)={x^2}+\frac{a}{x}$,函数的定义域为(-∞,0)∪(0,+∞),定义域关于原点对称,(1分)
①当a=0时,f(-x)=(-x)2=x2=f(x),
此时函数f(x)是偶函数; (2分)
②当a≠0时,f(1)=1+a,f(-1)=1-a,
此时f(1)≠f(-1)且f(1)+f(-1)≠0,
所以f(x)是非奇非偶函数.(4分)
(2)证明:?x1,x2∈(0,+∞),且x1<x2,则 (5分)
$f({x_1})-f({x_2})=({x_1^2+\frac{1}{x_1}})-({x_2^2+\frac{1}{x_2}})$=$({x_1^2-x_2^2})+({\frac{1}{x_1}-\frac{1}{x_2}})=({{x_1}-{x_2}})\frac{{({{x_1}+{x_2}}){x_1}{x_2}-1}}{{{x_1}{x_2}}}$,(6分)
当${x_1},{x_2}∈({0,\root{3}{{\frac{1}{2}}}})$时,$0<{x_1}+{x_2}<2\root{3}{{\frac{1}{2}}}$,$0<{x_1}{x_2}<\root{3}{{\frac{1}{4}}}$,
所以$0<({{x_1}+{x_2}}){x_1}{x_2}<2\root{3}{{\frac{1}{2}}}×\root{3}{{\frac{1}{4}}}=1$,
即$f({x_1})-f({x_2})=({{x_1}-{x_2}})\frac{{({{x_1}+{x_2}}){x_1}{x_2}-1}}{{{x_1}{x_2}}}<0$,
所以函数y=f(x)在区间$({0,\root{3}{{\frac{1}{2}}}})$上是单调递减函数; (8分)
同理:函数y=f(x)在区间$({\root{3}{{\frac{1}{2}}},+∞})$上是单调递增函数.(10分)
(3)因x+y2=z,x2+y=z2,所以
将x=z-y2代入x2+y=z2可得,(z-y2)2+y=z2,
整理得$2z={y^2}+\frac{1}{y}$(y>0),(13分)
由(2)知函数在区间$({0,\root{3}{{\frac{1}{2}}}})$上是单调递减函数,在区间$({\root{3}{{\frac{1}{2}}},+∞})$上是单调递增函数,
所以$2{z_{min}}={({\root{3}{{\frac{1}{2}}}})^2}+\frac{1}{{\root{3}{{\frac{1}{2}}}}}=\frac{3}{2}\root{3}{2}$,(15分)${z_{min}}=\frac{3}{4}\root{3}{2}$
此时$x=\frac{{\root{3}{2}}}{4}$,$y=\root{3}{{\frac{1}{2}}}$,代入原式,检验成立.(16分)
点评 本题主要考查函数奇偶性和单调性的判断和证明,以及函数最值的求解,综合考查函数的性质,综合性较强,有一定的难度.

| A. | {a|a=kπ+$\frac{π}{2}$,k∈Z} | B. | {a|a=kπ,k∈Z} | ||
| C. | {a|a=2kπ+$\frac{π}{2}$,k∈Z} | D. | {a|a=kπ或a=kπ+$\frac{π}{2}$,k∈Z} |
| A. | (-∞,-1)∪(0,1) | B. | (0,1)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (-1,0)∪(1,+∞) |
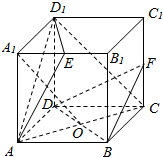 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.