题目内容
已知函数
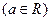 ,
,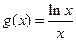 ,其中
,其中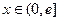 (1)若
(1)若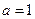 ,求
,求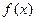 的极小值;(2)在(1)条件下证明
的极小值;(2)在(1)条件下证明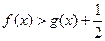 ;(3)是否存在实数
;(3)是否存在实数 ,使
,使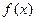 的最小值为3,如果存在,求出实数
的最小值为3,如果存在,求出实数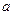 的值,若不存在,说明理由.
的值,若不存在,说明理由.

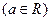 ,
,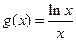 ,其中
,其中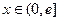 (1)若
(1)若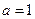 ,求
,求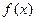 的极小值;(2)在(1)条件下证明
的极小值;(2)在(1)条件下证明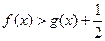 ;(3)是否存在实数
;(3)是否存在实数 ,使
,使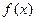 的最小值为3,如果存在,求出实数
的最小值为3,如果存在,求出实数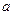 的值,若不存在,说明理由.
的值,若不存在,说明理由.(Ⅰ) f(x)的极小值为f(1)=1 (Ⅱ) 略 (Ⅲ)a=e2
:(1)∵f(x)=ax-lnx,f′(x)="1-" = ,∴当0<x<1时,f′(x)<0,此时f(x)单调递减;
当1<x<e时,f′(x)>0,此时f(x)单调递增。3分∴ f(x)的极小值为f(1)=1.4分
(2)∵f(x)的极小值为1,即f(x)在(0,e)上的最小值为1,∴f(x)>0,f(x)min=1.……6分
令h(x) = g(x)+ = + ,h′(x)=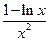 ,
,
当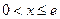 时,h′(x)>0,h(x)在
时,h′(x)>0,h(x)在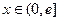 上单调递增,
上单调递增,
∴h(x) h(e)= +<+=1,…9分∴在(1)的条件下,f(x)>g(x)+.…10分
h(e)= +<+=1,…9分∴在(1)的条件下,f(x)>g(x)+.…10分
(3)假设存在实数a,使f (x) =ax-lnx ,x∈[0, e]有最小值3,f′(x)=a - = ,
(x) =ax-lnx ,x∈[0, e]有最小值3,f′(x)=a - = ,
①当0<<e时,f(x)在(0,)上单调递减,在(, e]上单调递增.
f(x)min= f()=1+ln a=3,a=e2,满足条件.……13分
a=3,a=e2,满足条件.……13分
②当≥e时,f(x)在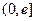 上
上 单调递减,f(x)min= f(e)=ae-1=3,a=(舍去),
单调递减,f(x)min= f(e)=ae-1=3,a=(舍去),
所以,此时f(x)无最小值.…15分
综上,存在实数a=e2,使得当x∈(0, e]时f(x)有最小值为3.…16分
当1<x<e时,f′(x)>0,此时f(x)单调递增。3分∴ f(x)的极小值为f(1)=1.4分
(2)∵f(x)的极小值为1,即f(x)在(0,e)上的最小值为1,∴f(x)>0,f(x)min=1.……6分
令h(x) = g(x)+ = + ,h′(x)=
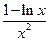 ,
,当
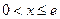 时,h′(x)>0,h(x)在
时,h′(x)>0,h(x)在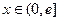 上单调递增,
上单调递增,∴h(x)
 h(e)= +<+=1,…9分∴在(1)的条件下,f(x)>g(x)+.…10分
h(e)= +<+=1,…9分∴在(1)的条件下,f(x)>g(x)+.…10分(3)假设存在实数a,使f
 (x) =ax-lnx ,x∈[0, e]有最小值3,f′(x)=a - = ,
(x) =ax-lnx ,x∈[0, e]有最小值3,f′(x)=a - = ,①当0<<e时,f(x)在(0,)上单调递减,在(, e]上单调递增.
f(x)min= f()=1+ln
 a=3,a=e2,满足条件.……13分
a=3,a=e2,满足条件.……13分②当≥e时,f(x)在
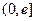 上
上 单调递减,f(x)min= f(e)=ae-1=3,a=(舍去),
单调递减,f(x)min= f(e)=ae-1=3,a=(舍去),所以,此时f(x)无最小值.…15分
综上,存在实数a=e2,使得当x∈(0, e]时f(x)有最小值为3.…16分

练习册系列答案
相关题目
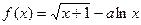 (
(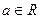 )
)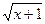
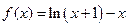 ,(1)求函数
,(1)求函数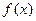 的单调减区间;(2)若
的单调减区间;(2)若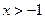 ,证明:
,证明: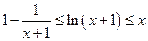 。
。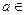 R,函数
R,函数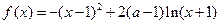 .(1) 若函数
.(1) 若函数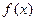 在点
在点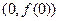 处的切线方程为
处的切线方程为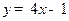 ,求a的值;(2) 当a<1时,讨论函数
,求a的值;(2) 当a<1时,讨论函数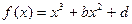 在(0,2)内是减函数,且2是方程
在(0,2)内是减函数,且2是方程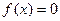 的根,则( )
的根,则( )



 已知函数
已知函数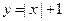 ,
,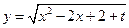 ,
,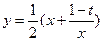
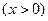 的最小值恰好是方程
的最小值恰好是方程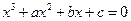 的三个根,其中
的三个根,其中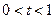 .
.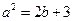 ;
;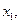
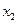 是函数
是函数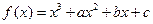 的两个极值点.若
的两个极值点.若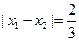 ,
,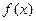 的解析式.
的解析式.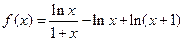 .
.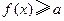 的解集为(0,+
的解集为(0,+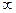 )?若存在,求a的取值范围;若不存在,试说明理由.
)?若存在,求a的取值范围;若不存在,试说明理由.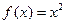 ,则
,则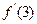 的值为( )
的值为( )



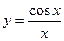 的导数是( )
的导数是( )


