题目内容
14．在正方体ABCD-A1B1C1D1中，平面ACB1的一个法向量为（ ）| A． | $\overrightarrow{B{D}_{1}}$ | B． | $\overrightarrow{DB}$ | C． | $\overrightarrow{B{A}_{1}}$ | D． | $\overrightarrow{B{B}_{1}}$ |
分析 由正方体的性质可得：BD1⊥B1C，BD1⊥AC．即可得出平面ACB1的一个法向量．
解答 解：如图所示，
由正方体的性质可得：BD1⊥B1C，BD1⊥AC．
∴BD1⊥平面ACB1．
∴平面ACB1的一个法向量为$\overrightarrow{B{D}_{1}}$．
故选：A．
点评 本题考查了线面垂直的判定与性质、平面的法向量，考查了推理能力与计算能力．
练习册系列答案
备战中考寒假系列答案
相关题目
4．
如图是函数y=sin（ωx+φ）（ω＞0，0＜φ＜$\frac{π}{2}$）在区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的图象，将该图象向右平移m（m＞0）个单位后，所得图象关于直线x=$\frac{π}{4}$对称，则m的最小值为（ ）
如图是函数y=sin（ωx+φ）（ω＞0，0＜φ＜$\frac{π}{2}$）在区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的图象，将该图象向右平移m（m＞0）个单位后，所得图象关于直线x=$\frac{π}{4}$对称，则m的最小值为（ ）| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$ |
2．设实数x，y满足不等式组$\left\{{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥-1}\end{array}}\right.$．则z=3x+y的取值范围是（ ）
| A． | [-4，0] | B． | [0，4] | C． | [-2，4] | D． | [-4，4] |
9．一个口袋中有编号分别为0，1，2的小球各2个，从这6个球中任取2个，则取出2个球的编号数和的期望为（ ）
| A． | 1 | B． | 1.5 | C． | 2 | D． | 2.5 |
19．在△ABC中，角A，B，C的对边为a，b，c，b=8，c=8$\sqrt{3}$，S△ABC=16$\sqrt{3}$，则A等于（ ）
| A． | 30° | B． | 60° | C． | 30°或150° | D． | 60°或120° |
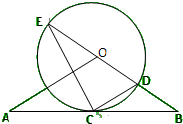（如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，连接EC，CD．
如图，在圆内接四边形ABCD中，AB∥DC，过点A作圆的切线与CB的延长线交于点E．若AB=AD=BC=5，AE=6，则DC=$\frac{25}{4}$．