题目内容
5.正三棱柱ABC-A1B1C1中,所有棱长都等于a,D点为BC的中点.(1)求证:A1B∥平面AC1D;
(2)点C到平面ADC1的距离.
分析 (1)连接A1C,交AC1于O,连接OD,运用中位线定理,以及直线和平面平行的判定定理,即可得证;
(2)利用等体积,求点C到平面ADC1的距离.
解答 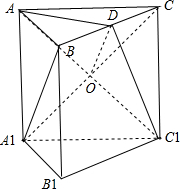 (1)证明:连接A1C,交AC1于O,连接OD,
(1)证明:连接A1C,交AC1于O,连接OD,
由于OD是△A1BC的中位线,则OD∥A1B,
又OD?平面面AC1D,A1B?平面AC1D,
则有A1B∥平面AC1D;
(2)解:设点C到平面ADC1的距离为h,则
由等体积可得$\frac{1}{2}×\frac{\sqrt{3}}{2}a×\sqrt{{a}^{2}+\frac{{a}^{2}}{4}}×h$=$\frac{1}{2}×\frac{a}{2}×\frac{\sqrt{3}}{2}a×a$,
∴h=$\frac{\sqrt{5}}{5}$a.
点评 本题考查线面平行的判定定理,考查学生分析解决问题的能力,注意运用体积转换法,属于中档题.

练习册系列答案
相关题目
16.斜率为$\frac{{\sqrt{2}}}{2}$的直线与焦点在x轴上的双曲线x2-$\frac{y^2}{b^2}$=1(b>0)交于不同的两点P、Q.若点P、Q在x轴上的投影恰好为双曲线的两焦点,则该双曲线的焦距为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
10.若复数z满足z(1+i)=4-2i(i为虚数单位),则|z|=( )
| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
14.在正方体ABCD-A1B1C1D1中,平面ACB1的一个法向量为( )
| A. | $\overrightarrow{B{D}_{1}}$ | B. | $\overrightarrow{DB}$ | C. | $\overrightarrow{B{A}_{1}}$ | D. | $\overrightarrow{B{B}_{1}}$ |
15.设全集U=R,A={x|x<1},B={x|log2x<1},则A∩B=( )
| A. | {x|0<x<1} | B. | {x|0<x<2} | C. | {x|-1<x<1} | D. | {x|-1<x<2} |