题目内容
在空间直角坐标系O-xyz中,平面OAB的法向量为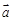 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
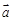 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )| A.4 | B.2 | C.3 | D.1 |
B
试题分析:因为向量
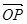 在平面OAB的法向量投影的绝对值为P到平面OAB的距离,所以
在平面OAB的法向量投影的绝对值为P到平面OAB的距离,所以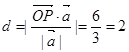 .
.
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
题目内容
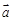 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )| A.4 | B.2 | C.3 | D.1 |
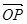 在平面OAB的法向量投影的绝对值为P到平面OAB的距离,所以
在平面OAB的法向量投影的绝对值为P到平面OAB的距离,所以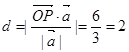 .
.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案